题目内容
19.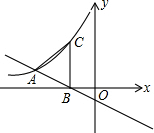 直线y=-$\frac{1}{2}$x-1与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为-4.
直线y=-$\frac{1}{2}$x-1与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为-4.
分析 过A作AD⊥BC于D,先求出直线=-$\frac{1}{2}$x-1与x轴交点B的坐标(-2,0),则得到C点的横坐标为-2,由于C点在反比例函数y=$\frac{k}{x}$的图象上,可表示出C点坐标为(-2,-$\frac{k}{2}$),利用等腰三角形的性质,由AC=AB,AD⊥BC,得到DC=DB,于是D点坐标为(-2,-$\frac{k}{4}$),则可得到A点的纵坐标为-$\frac{k}{4}$,利用点A在函数y=$\frac{k}{x}$的图象上,可表示出点A的坐标为(-4,-$\frac{k}{4}$),然后把A(-4,-$\frac{k}{4}$)代入y=-$\frac{1}{2}$x-1得到关于k的方程,解方程即可求出k的值.
解答 解:过A作AD⊥BC于D,如图,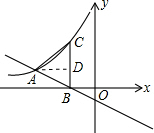
∵y=-$\frac{1}{2}$x-1,
令y=0,则-$\frac{1}{2}$x-1=0,解得x=-2,
∴B点坐标为(-2,0),
∵CB⊥x轴,
∴C点的横坐标为-2,
∵y=$\frac{k}{x}$,令x=-2,则y=-$\frac{k}{2}$,
∴C点坐标为(-2,-$\frac{k}{2}$),
∵AC=AB,AD⊥BC,
∴DC=DB,
∴D点坐标为(-2,-$\frac{k}{4}$),
∴A点的纵坐标为-$\frac{k}{4}$,
而点A在函数y=$\frac{k}{x}$的图象上,
把y=-$\frac{k}{4}$代入y=$\frac{k}{x}$,得x=-4,
∴点A的坐标为(-4,-$\frac{k}{4}$),
把A(-4,-$\frac{k}{4}$)代入y=-$\frac{1}{2}$x-1,得-$\frac{k}{4}$=-$\frac{1}{2}$×(-4)-1,
∴k=-4.
故答案为-4.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两个函数的解析式.也考查了与x轴垂直的直线上所有点的横坐标相同以及等腰三角形的性质.

| A. | 变大 | B. | 变小 | C. | 不变 | D. | 无法确定 |
 如图所示几何体的左视图是( )
如图所示几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
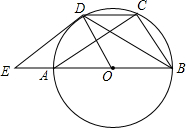 如图,⊙O是△ABC的外接圆,AB是直径,点D是$\widehat{AC}$的中点,E为BA延长线上一点,且∠DEB=∠CDB
如图,⊙O是△ABC的外接圆,AB是直径,点D是$\widehat{AC}$的中点,E为BA延长线上一点,且∠DEB=∠CDB