题目内容
9.解不等式(组)(1)$\frac{1}{2}(2-x)>\frac{1}{4}(3-x)+\frac{1}{8}$
(2)$\left\{\begin{array}{l}x+4≤3(x+2)\\ \frac{x-1}{2}<\frac{x}{3}\end{array}\right.$.
分析 (1)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)去分母,得:4(2-x)>2(3-x)+1,
去括号,得:8-4x>6-2x+1,
移项、合并,得:-2x>-1,
系数化为1,得:x<$\frac{1}{2}$;
(2)解不等式x+4≤3(x+2),得:x≥-1
解不等式$\frac{x-1}{2}<\frac{x}{3}$,得:x<3
∴原不等式组的解为-1≤x<3.
点评 本题考查的是解一元一次不等式、不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
19.2015年济南生产总值(GDP)达6280亿元,在全国排第21名,在山东排第3名.6280用科学记数法表示为( )
| A. | 62.8×102 | B. | 6.28×103 | C. | 0.628×104 | D. | 6.28×102 |
20. 如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=4cm,△ADC的周长为15cm,则BC的长( )
如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=4cm,△ADC的周长为15cm,则BC的长( )
 如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=4cm,△ADC的周长为15cm,则BC的长( )
如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=4cm,△ADC的周长为15cm,则BC的长( )| A. | 8cm | B. | 11cm | C. | 13cm | D. | 19cm |
17.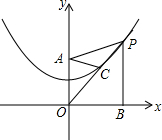 如图,点P是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的点,线段PO交抛物线于点C,PB⊥x轴于点B,点A的坐标是(0,2),当点C是OP的中点时,下列说法错误的是( )
如图,点P是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的点,线段PO交抛物线于点C,PB⊥x轴于点B,点A的坐标是(0,2),当点C是OP的中点时,下列说法错误的是( )
 如图,点P是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的点,线段PO交抛物线于点C,PB⊥x轴于点B,点A的坐标是(0,2),当点C是OP的中点时,下列说法错误的是( )
如图,点P是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的点,线段PO交抛物线于点C,PB⊥x轴于点B,点A的坐标是(0,2),当点C是OP的中点时,下列说法错误的是( )| A. | PA=PB | B. | ∠POB=45° | C. | PA=2AC | D. | PB=3 |
1.自从扫描隧道显微镜发明以后,世界上便诞生了一门新兴的学科,这就是“纳米技术”,已知1纳米=0.000000001米,则2.25纳米用科学记数法表示为( )
| A. | 2.25×10-8 米 | B. | 0.225×10-10米 | C. | 2.25×10-10米 | D. | 2.25×10-9米 |
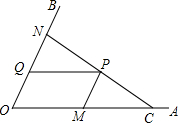 如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点 Q,PM∥OB交OA于点M.
如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点 Q,PM∥OB交OA于点M.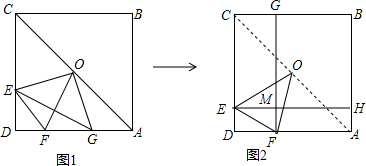
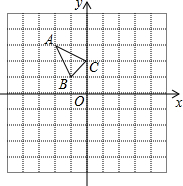 △ABC在平面直角坐标系xOy中的位置如图所示.
△ABC在平面直角坐标系xOy中的位置如图所示.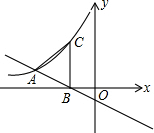 直线y=-$\frac{1}{2}$x-1与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为-4.
直线y=-$\frac{1}{2}$x-1与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为-4.