题目内容
11.若关于x的不等式组$\left\{\begin{array}{l}{2x+a>3}\\{5x-b<2}\end{array}\right.$的解集是-1<x<2,则ab=40.分析 解关于x的不等式组,根据不等式组的解集-1<x<2可得关于a、b的方程组,解方程组得a、b的值,代入求值可得.
解答 解:解不等式2x+a>3,得:x>$\frac{3-a}{2}$,
解不等式5x-b<2,得:x<$\frac{2+b}{5}$,
∵不等式组的解集是-1<x<2,
∴$\left\{\begin{array}{l}{\frac{3-a}{2}=-1}\\{\frac{2+b}{5}=2}\end{array}\right.$,
解得:a=5,b=8,
∴ab=5×8=40,
故答案为:40.
点评 本题主要考查解不等式和方程组的能力,求出每个不等式的解集是根本和前提,结合不等式组的解集得出关于a、b的方程组是解题的关键.

练习册系列答案
相关题目
1.自从扫描隧道显微镜发明以后,世界上便诞生了一门新兴的学科,这就是“纳米技术”,已知1纳米=0.000000001米,则2.25纳米用科学记数法表示为( )
| A. | 2.25×10-8 米 | B. | 0.225×10-10米 | C. | 2.25×10-10米 | D. | 2.25×10-9米 |
2.统计显示,2015年汕头市中考学生人数和高考学生人数合计大约是13.3万人,将13.3万用科学记数法表示应为( )
| A. | 13.3×102 | B. | 1.33×103 | C. | 1.33×104 | D. | 1.33×105 |
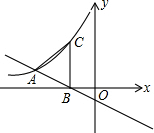 直线y=-$\frac{1}{2}$x-1与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为-4.
直线y=-$\frac{1}{2}$x-1与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为-4.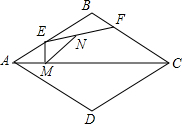 如图,菱形ABCD的边长为8,∠BAD=60°,点E在AB上运动,点F在BC上运动(E,F两点可以和菱形的顶点重合),且EF=4,点N是线段EF的中点,ME⊥AC垂足为M,则MN的最小值是2$\sqrt{3}$.
如图,菱形ABCD的边长为8,∠BAD=60°,点E在AB上运动,点F在BC上运动(E,F两点可以和菱形的顶点重合),且EF=4,点N是线段EF的中点,ME⊥AC垂足为M,则MN的最小值是2$\sqrt{3}$.