题目内容
7. 如图,AB是⊙O的直径,点C、D在⊙O上,且AC平分∠BAD,点E为AB的延长线上一点,且∠ECB=∠CAD.
如图,AB是⊙O的直径,点C、D在⊙O上,且AC平分∠BAD,点E为AB的延长线上一点,且∠ECB=∠CAD.(1)①填空:∠ACB=90°,理由是直径所对的圆周角是直角;
②求证:CE与⊙O相切;
(2)若AB=6,CE=4,求AD的长.
分析 (1)①根据圆周角定理即可求得;
②连接OC.欲证明CE是⊙O的切线,只需证明CE⊥OC即可;
(2)根据弦切角定理求得BE,进一步求得AC=2BC,根据勾股定理求得AC和BC的值,进一步证得△ADC∽△CBE,得出$\frac{AD}{BC}$=$\frac{AC}{CE}$,即$\frac{AD}{\frac{6\sqrt{5}}{5}}$=$\frac{\frac{12\sqrt{5}}{5}}{4}$,即可求得AD的长.
解答 解:①∵AB为⊙O的直径,
∴∠ACB=90°,
故答案为90°,直径所对的圆周角是直角;
②连接OC,则∠CAO=∠ACO,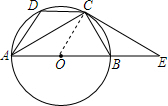 ∵AC平分∠BAB,
∵AC平分∠BAB,
∴∠BAC=∠CAD,
∵∠ECB=∠CAD.
∴∠BAC=∠ECB.
∴∠ECB=∠ACO,
∵∠ACO+∠OCB=90°,
∴∠ECB+∠OCB=90°,即CE⊥OC.
∴CE与⊙O相切;
(2)∵CE与⊙O相切,
∴CE2=BE•AE,
∵AB=6,CE=4,
∴42=BE(BE+6),
∴BE=2,
∴AE=6+2=8,
∵△ACE∽△CBE,
∴$\frac{AC}{BC}$=$\frac{CE}{BE}$,即$\frac{AC}{BC}$=$\frac{4}{2}$=2,
∴AC=2BC,
∵AC2+BC2=AB2,
∴5BC2=36,
∴BC=$\frac{6\sqrt{5}}{5}$,
∴AC=$\frac{12\sqrt{5}}{5}$.
∵∠ECB=∠CAD,∠CBE=∠D,
∴△ADC∽△CBE,
∴$\frac{AD}{BC}$=$\frac{AC}{CE}$,即$\frac{AD}{\frac{6\sqrt{5}}{5}}$=$\frac{\frac{12\sqrt{5}}{5}}{4}$
∴AD=$\frac{18}{5}$.
点评 本题考查了切线的判定与性质,等腰三角形的判定和性质,相似三角形的性质等;证明某一线段是圆的切线时,一般情况下是连接切点与圆心,通过证明该半径垂直于这一线段来判定切线.

| A. | $\frac{3}{28}$ | B. | $\frac{5}{28}$ | C. | $\frac{3}{56}$ | D. | $\frac{5}{56}$ |
 如图,已知在四边形ABCD中,AE,BD于EE,CF,BD于F,AE=CF,BF=DE,求证:四边形ABCD是平行四边形.
如图,已知在四边形ABCD中,AE,BD于EE,CF,BD于F,AE=CF,BF=DE,求证:四边形ABCD是平行四边形.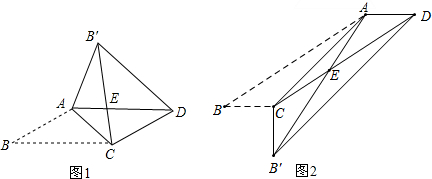
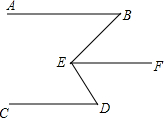 如图,已知∠B=∠BEF,EF∥CD,试判断AB与CD是否平行?
如图,已知∠B=∠BEF,EF∥CD,试判断AB与CD是否平行?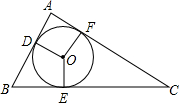 如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的大小.
如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的大小.