题目内容
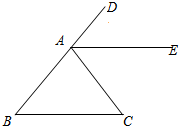 如图,∠DAC是△ABC的一个外角,AE平分∠DAC,且AE∥BC,那么AB与AC相等吗?为什么?
如图,∠DAC是△ABC的一个外角,AE平分∠DAC,且AE∥BC,那么AB与AC相等吗?为什么?考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:利用平行和角平分线可求得∠B=∠C,即可得到AB=AC.
解答:解:相等,理由如下:
∵AE∥BC,
∴∠DAE=∠B,∠EAC=∠C,
∵AE平分∠DAC,
∴∠DAE=∠EAC,
∴∠B=∠C,
∴AB=AC.
∵AE∥BC,
∴∠DAE=∠B,∠EAC=∠C,
∵AE平分∠DAC,
∴∠DAE=∠EAC,
∴∠B=∠C,
∴AB=AC.
点评:本题主要考查等腰三角形的判定,掌握等角对等边是解题的关键,注意平行线的性质的应用.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
将直线y=-2x+3向下平移2个单位所得的直线解析式是( )
| A、y=-2x+7 |
| B、y=-2x+5 |
| C、y=-2x-1 |
| D、y=-2x+1 |
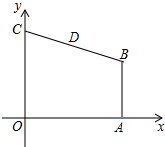 已知:如图,在直角梯形COAB中,OC∥AB,∠AOC=90°,AB=4,AO=8,OC=10,以O为原点建立平面直角坐标系,点D为线段BC的中点.动点P从点A出发,以每秒4个单位的速度,沿折线AO-OC-CD向终点D运动,设运动时间为t秒.
已知:如图,在直角梯形COAB中,OC∥AB,∠AOC=90°,AB=4,AO=8,OC=10,以O为原点建立平面直角坐标系,点D为线段BC的中点.动点P从点A出发,以每秒4个单位的速度,沿折线AO-OC-CD向终点D运动,设运动时间为t秒. 已知:如图,在△ABC中,∠ABC和∠ACB的平分线交于点D.过点D作EF∥BC交AB于点E,交AC于点F,若BE+CF=9cm,求线段EF的长.
已知:如图,在△ABC中,∠ABC和∠ACB的平分线交于点D.过点D作EF∥BC交AB于点E,交AC于点F,若BE+CF=9cm,求线段EF的长.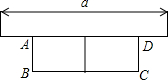 如图,有长为24米的篱笆,一面利用墙(强的最大可用长度为a为12米),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,花圃ABCD的面积为S米2.
如图,有长为24米的篱笆,一面利用墙(强的最大可用长度为a为12米),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,花圃ABCD的面积为S米2.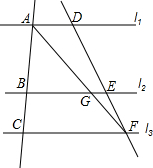 如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长.
如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长.