题目内容
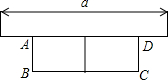如图，有长为24米的篱笆，一面利用墙（强的最大可用长度为a为12米），围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，花圃ABCD的面积为S米2．（1）当x为何值时，花圃ABCD的面积最大？最大面积是多少？
（2）如果要围成面积为45米2的花圃，AB的长是多少米？
考点：一元二次方程的应用,二次函数的应用
专题：几何图形问题
分析：（1）用总长减去三个宽即为BC的长，进而表示出矩形面积，求出最值即可；
（2）利用矩形的面积公式列出方程求解即可．
（2）利用矩形的面积公式列出方程求解即可．
解答：解：（1）由题意可得：
S=x（24-3x）
=-3x2+24x
=-3（x-4）2+48，
当x=4时，面积最大，最大面积为48m2；
（2）由条件-3x2+24x=45化为x2-8x+15=0
解得x1=5，x2=3，
当x=3时，BC=24-3x=15＞10，不合题意，舍去，
当x=5时，BC=24-3x=9，
如果要围成面积为45米2的花圃，AB的长是5米．
S=x（24-3x）
=-3x2+24x
=-3（x-4）2+48，
当x=4时，面积最大，最大面积为48m2；
（2）由条件-3x2+24x=45化为x2-8x+15=0
解得x1=5，x2=3，
当x=3时，BC=24-3x=15＞10，不合题意，舍去，
当x=5时，BC=24-3x=9，
如果要围成面积为45米2的花圃，AB的长是5米．
点评：本题考查了一元二次方程、二次函数的应用，根据已知条件列出二次函数式是解题的关键．
练习册系列答案
相关题目
如图所示，有一块边长为24m的正方形绿地，绿地周边是小路，在绿地旁边的B处有健身器材，BC=7m．请你算一算，如果居住在A处的居民为了走近路而不惜践踏草地直接从A到B，这样比沿着绿地周边的小路，仅少走多少米？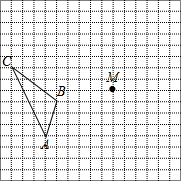
如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）和点M．
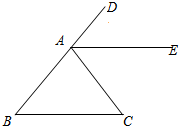如图，∠DAC是△ABC的一个外角，AE平分∠DAC，且AE∥BC，那么AB与AC相等吗？为什么？