题目内容
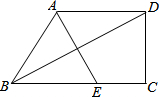 如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是
如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是考点:梯形
专题:
分析:连接DE,因为AB=AD,AE⊥BD,AD∥BC,可证四边形ABED为菱形,从而得到BE、BC的长,继而求出梯形ABCD的周长.
解答:解:连接DE.
在直角三角形CDE中,EC=3cm,CD=4cm,根据勾股定理,得DE=5cm.
∵AB=AD,AE⊥BD,
∴AE垂直平分BD,∠BAE=∠DAE.
∴DE=BE=5cm.
∵AD∥BC,
∴∠DAE=∠AEB,
.∴∠BAE=∠AEB,
∴AB=BE=5cm,
∴BC=BE+EC=8,
∴梯形ABCD的周长=AB+AD+BC+DC=5+5+8+4=22cm,
故答案为:22.
在直角三角形CDE中,EC=3cm,CD=4cm,根据勾股定理,得DE=5cm.

∵AB=AD,AE⊥BD,
∴AE垂直平分BD,∠BAE=∠DAE.
∴DE=BE=5cm.
∵AD∥BC,
∴∠DAE=∠AEB,
.∴∠BAE=∠AEB,
∴AB=BE=5cm,
∴BC=BE+EC=8,
∴梯形ABCD的周长=AB+AD+BC+DC=5+5+8+4=22cm,
故答案为:22.
点评:本题考查梯形的性质、勾股定理的运用以及菱形的判定和性质,题目难度适中,根据条件能够发现图中的菱形ABDE是关键.

练习册系列答案
相关题目
 如图,在五边形ABCDE中,AB∥DE,若△ABE的面积为5,则△ABD的面积为( )
如图,在五边形ABCDE中,AB∥DE,若△ABE的面积为5,则△ABD的面积为( )| A、4 | B、5 | C、10 | D、无法判断 |
 已知抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线x=
已知抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线x= 如图,取一张正方形纸片ABCD四条边的中点E,F,G,H,连结AF,BG,CH,DE.沿这些连线剪4刀,便剪出中间这个较小的正方形(阴影部分).请试一试,若要剪出的小正方形的边长为
如图,取一张正方形纸片ABCD四条边的中点E,F,G,H,连结AF,BG,CH,DE.沿这些连线剪4刀,便剪出中间这个较小的正方形(阴影部分).请试一试,若要剪出的小正方形的边长为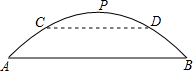 如图,有一座拱桥是抛物线形,它的跨度AB为60米,拱桥最高处点P到AB的距离为18米,
如图,有一座拱桥是抛物线形,它的跨度AB为60米,拱桥最高处点P到AB的距离为18米, 如图,在△ABC中,AB=AC,AD⊥BC于点D,点P在BC上,PE⊥BC,交BA的延长线于点E,交AC于点F.求证:2AD=PE+PF.
如图,在△ABC中,AB=AC,AD⊥BC于点D,点P在BC上,PE⊥BC,交BA的延长线于点E,交AC于点F.求证:2AD=PE+PF. 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).将△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).将△AOB绕点O逆时针旋转90°后得到△A1OB1.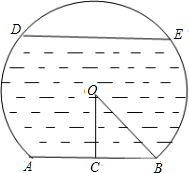 一个弓形桥洞截面示意图如图所示,圆心为O,弦AB是水底线,OC⊥AB,AB=24m,sin∠COB=
一个弓形桥洞截面示意图如图所示,圆心为O,弦AB是水底线,OC⊥AB,AB=24m,sin∠COB=