题目内容
某种产品每件成本为18元,试销中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100(利润.(利润=售价-成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)根据每月的利润z=(x-18)y,再把y=-2x+100代入即可求出z与x之间的函数解析式;
(2)将z=-2x2+136x-1800配方,得z=-2(x-34)2+512,即可求出当销售单价为多少元时,厂商每月能获得最大利润,最大利润是多少.
(2)将z=-2x2+136x-1800配方,得z=-2(x-34)2+512,即可求出当销售单价为多少元时,厂商每月能获得最大利润,最大利润是多少.
解答:解:(1)z=(x-18)y=(x-18)(-2x+100)
=-2x2+136x-1800,
∴z与x之间的函数解析式为z=-2x2+136x-1800(x>18);
(2)将z=-2x2+136x-1800配方,得z=-2(x-34)2+512(x>18).
答:当销售单价为34元时,每月能获得最大利润,最大利润是512万元;
=-2x2+136x-1800,
∴z与x之间的函数解析式为z=-2x2+136x-1800(x>18);
(2)将z=-2x2+136x-1800配方,得z=-2(x-34)2+512(x>18).
答:当销售单价为34元时,每月能获得最大利润,最大利润是512万元;
点评:本题考查的是二次函数在实际生活中的应用,关键是根据题意求出二次函数的解析式,综合利用二次函数和一次函数的性质解决实际问题.

练习册系列答案
相关题目
36的平方根( )
| A、±4 | B、±6 | C、6 | D、4 |
某工程需在规定日期内完成,若甲工程队独做,恰好如期完成,如果乙工程队独做,则超过规定日期3天完成,现在甲、乙两队合作2天,剩下的由乙队独做,恰好在规定日期完成,求规定日期,如果设规定日期为x天,则下列正确( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需要( )
| A、(4m+7n)元 |
| B、28mn元 |
| C、(7m+4n)元 |
| D、11mn元 |
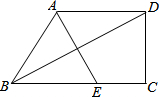 如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是
如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是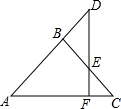 如图,△ABC,AB=BC,DF⊥AC于F,交AB的延长线于D,求证:△DBE是等腰三角形.
如图,△ABC,AB=BC,DF⊥AC于F,交AB的延长线于D,求证:△DBE是等腰三角形.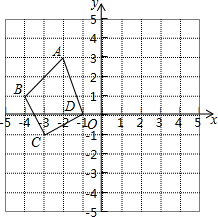 如图,利用关于原点对称的点的坐标的特点,作出与四边形ABCD关于原点对称的图形.
如图,利用关于原点对称的点的坐标的特点,作出与四边形ABCD关于原点对称的图形.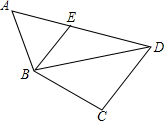 如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的中垂线上,则∠ADC的度数为( )
如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的中垂线上,则∠ADC的度数为( )