题目内容
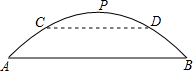 如图,有一座拱桥是抛物线形,它的跨度AB为60米,拱桥最高处点P到AB的距离为18米,
如图,有一座拱桥是抛物线形,它的跨度AB为60米,拱桥最高处点P到AB的距离为18米,(1)建立恰当的坐标系,求出抛物线的解析式;
(2)当洪水泛滥,水面上升,若拱桥的水面跨度只有30米时,则必须马上采取紧急措施.现已知拱顶P离水面CD的距离只有4米,问:是否要采取紧急措施?并说明理由.
考点:二次函数的应用
专题:
分析:(1)以AB所在直线为x轴,过P点⊥x轴的直线为y轴建立平面直角坐标系,表示出点P和点B的坐标,利用待定系数法确定二次函数的解析式即可;
(2)求得点E的坐标,然后求得点C和点D的横坐标,从而确定CD的长,与30米比较后即可确定是否采取紧急措施.
(2)求得点E的坐标,然后求得点C和点D的横坐标,从而确定CD的长,与30米比较后即可确定是否采取紧急措施.
解答:解: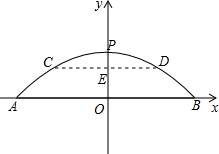 (1)如图建立平面直角坐标系,
(1)如图建立平面直角坐标系,
由题意得:P(0,18)B(30,0),
设抛物线的解析式为:y=ax2+18,
把B(30,0)代入计算得:0=900a+18,
解得:a=-
,
所以二次函数的解析式为y=-
x2+18;
(2)要采取紧急措施;
由题意得:CD与y轴交点E坐标为(0,14),
代入抛物线y=-
x2+18得:x=±10
,
故CD=20
米<30米,要采取紧急措施.
 (1)如图建立平面直角坐标系,
(1)如图建立平面直角坐标系,由题意得:P(0,18)B(30,0),
设抛物线的解析式为:y=ax2+18,
把B(30,0)代入计算得:0=900a+18,
解得:a=-
| 1 |
| 50 |
所以二次函数的解析式为y=-
| 1 |
| 50 |
(2)要采取紧急措施;
由题意得:CD与y轴交点E坐标为(0,14),
代入抛物线y=-
| 1 |
| 50 |
| 2 |
故CD=20
| 2 |
点评:本题考查了二次函数的解析式,解题的关键是建立适当的坐标系求得二次函数的解析式,难度不大,是中考的热点考题之一.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
36的平方根( )
| A、±4 | B、±6 | C、6 | D、4 |
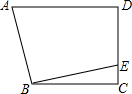 如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )
如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )| A、6 | B、8 | C、10 | D、无法确定 |
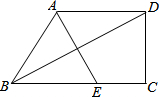 如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是
如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是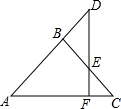 如图,△ABC,AB=BC,DF⊥AC于F,交AB的延长线于D,求证:△DBE是等腰三角形.
如图,△ABC,AB=BC,DF⊥AC于F,交AB的延长线于D,求证:△DBE是等腰三角形.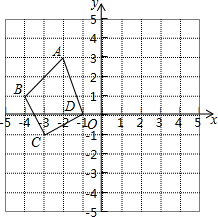 如图,利用关于原点对称的点的坐标的特点,作出与四边形ABCD关于原点对称的图形.
如图,利用关于原点对称的点的坐标的特点,作出与四边形ABCD关于原点对称的图形.