题目内容
14.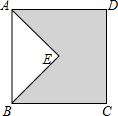 如图,四边形ABCD是正方形,AE垂直于BE,AE=3,BE=4,则图中阴影部分的面积是19.
如图,四边形ABCD是正方形,AE垂直于BE,AE=3,BE=4,则图中阴影部分的面积是19.
分析 由AE垂直于BE,AE=3,BE=4,利用勾股定理可求得AB的长,继而求得正方形ABCD的面积与△ABE的面积,则可求得答案.
解答 解:∵AE垂直于BE,AE=3,BE=4,
∴AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=5,
∵四边形ABCD是正方形,
∴S阴影=S正方形ABCD-S△ABE=25-$\frac{1}{2}$×3×4=19.
故答案为:19.
点评 此题考查了正方形的性质与勾股定理.注意利用勾股定理求得AE的长是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
4.以下各组数为三角形的三条边长,其中能作成直角三角形的是( )
| A. | 2,$\sqrt{2}$,4 | B. | 4,5,6 | C. | 2,3,4 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
9.如果直角三角形两直角边为5:12,则斜边上的高与斜边的比为( )
| A. | 60:13 | B. | 5:12 | C. | 12:13 | D. | 60:169 |
6.“六•一”儿童节前夕,某超市用3000元购进A、B两种童装共120件,其中A种童装每件24元,B种童装每件30元.若设购买A种童装x件,B种童装y件,依题意列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=120}\\{24x+30y=3000}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=120}\\{30x+24y=300}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{30x+24y=120}\\{x+y=3000}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{24x+30y=120}\\{x+y=3000}\end{array}\right.$ |
 如图,AD为△ABC的中线,E是AD的中点,若△ABC的面积为40,BD=5,则△BDE中BD边上的高为4.
如图,AD为△ABC的中线,E是AD的中点,若△ABC的面积为40,BD=5,则△BDE中BD边上的高为4.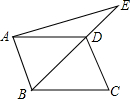 如图,点E在平行四边形ABCD的对角线BD的延长线上.
如图,点E在平行四边形ABCD的对角线BD的延长线上. 如图,直线l与直线a,b相交,且a∥b,∠1=45°,则∠2的度数是45°.
如图,直线l与直线a,b相交,且a∥b,∠1=45°,则∠2的度数是45°.