题目内容
4．以下各组数为三角形的三条边长，其中能作成直角三角形的是（ ）| A． | 2，$\sqrt{2}$，4 | B． | 4，5，6 | C． | 2，3，4 | D． | 1，$\sqrt{2}$，$\sqrt{3}$ |
分析 由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
解答 解：A、∵22+（$\sqrt{2}$）2=6≠42，故此选项错误；
B、∵42+52=41≠62，故此选项错误；
C、∵22+32=13≠42，故此选项错误；
D、∵12+（$\sqrt{2}$）2=3=（$\sqrt{3}$）2，故此选项正确．
故选D．
点评 本题考查直角三角形的判定，利用勾股定理的逆定理是解答此题的关键．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
如图，在Rt△ABC中，∠ACB=90°，D、E、F分别是AB、BC、CA的中点，若CD=5cm，求EF的长．
16．在平面直角坐标系xOy中，对于点P（a，b）和点Q（a，b′），给出下列定义：若b′=$\left\{\begin{array}{l}{b，}&{a≥1}\\{-b，}&{a＜1}\end{array}\right.$，则称点Q为点的限变点．例如：点（2，3）的限变点的坐标是（2，3），点（-2，5）的限变点的坐标是（-2，-5），如果一个点的限变点的坐标是（$\sqrt{3}$，-1），那么这个点的坐标是（ ）
| A． | （-1，$\sqrt{3}$） | B． | （-$\sqrt{3}$，-1） | C． | （$\sqrt{3}$，-1） | D． | （$\sqrt{3}$，1） |
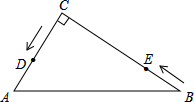如图，在△ABC中，∠C=90°，AC=6cm，BC=8cm，点D从点C出发，以2cm/s的速度沿折线C→A→B向点B运动，同时，点E从点B出发，以1cm/s的速度沿BC边向点C运动，设点E运动的时间为ts（0＜t＜8）．
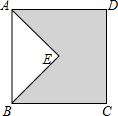如图，四边形ABCD是正方形，AE垂直于BE，AE=3，BE=4，则图中阴影部分的面积是19．