题目内容
19.已知一个直角三角形的两条直角边的长度之比为1:2,斜边长为$\sqrt{50}$,求这个直角三角形的面积.分析 此题要先设出直角边的长,根据勾股定理列出方程求解,最后根据其直角边的长求出面积即可.
解答 解:设较短的直角边为x,则另一直角边为2x,
由勾股定理得x2+(2x)2=50.解得x=$\sqrt{10}$.
所以直角三角形的面积为:$\frac{1}{2}$×$\sqrt{10}$×2$\sqrt{10}$=10.
点评 本题考查了利用勾股定理解直角三角形的能力,此题属简单题目,熟记勾股定理是解题关键.

练习册系列答案
相关题目
10.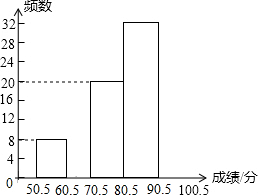 某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:
某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:
(1)求a的值,并补全频数分布直方图.
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
 某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:
某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:| 分组 | 频数 | 频率 |
| 50.5-60.5 | 8 | 0.08 |
| 60.5-70.5 | 12 | 0.12 |
| 70.5-80.5 | 20 | 0.2 |
| 80.5-90.5 | 32 | 0.32 |
| 90.5-100.5 | 28 | a |
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
4.下列命题中,是假命题的是( )
| A. | 等角的余角相等 | B. | 若a>b,且m≠0,则am>bm | ||
| C. | 三角形的外角和等于360° | D. | 两直线平行,同位角相等 |
11.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.在函数y=$\sqrt{x-1}$中,x的取值范围是( )
| A. | x≥1 | B. | x≤1 | C. | x≠1 | D. | x<0 |
 如图,在矩形ABCD中,AB=4,BC=8,Rt△EFG中,EF=4,EG=3,∠GEF=90°,与点B与点E重合时,将△EFG绕点E顺时针旋转α(0°<α<90°),直线FG分别与直线AD、BD相交于M、N,当△DMN是直角三角形时,线段MN的值是2$\sqrt{5}$-$\frac{6}{5}$或$\frac{14}{5}$.
如图,在矩形ABCD中,AB=4,BC=8,Rt△EFG中,EF=4,EG=3,∠GEF=90°,与点B与点E重合时,将△EFG绕点E顺时针旋转α(0°<α<90°),直线FG分别与直线AD、BD相交于M、N,当△DMN是直角三角形时,线段MN的值是2$\sqrt{5}$-$\frac{6}{5}$或$\frac{14}{5}$.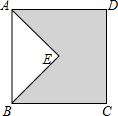 如图,四边形ABCD是正方形,AE垂直于BE,AE=3,BE=4,则图中阴影部分的面积是19.
如图,四边形ABCD是正方形,AE垂直于BE,AE=3,BE=4,则图中阴影部分的面积是19. 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE.延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④△GCF是等边三角形,其中正确结论有①②③.
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE.延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④△GCF是等边三角形,其中正确结论有①②③.