题目内容
2.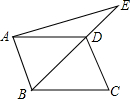 如图,点E在平行四边形ABCD的对角线BD的延长线上.
如图,点E在平行四边形ABCD的对角线BD的延长线上.(1)填空:$\overrightarrow{DA}$+$\overrightarrow{DC}$=$\overrightarrow{DB}$.$\overrightarrow{AE}$-$\overrightarrow{BC}$=$\overrightarrow{DE}$;
(2)求作:$\overrightarrow{AB}$+$\overrightarrow{DE}$(不写作法,保留作图痕迹,写出结果)
分析 (1)根据向量的平行四边形法则写出$\overrightarrow{DA}$+$\overrightarrow{DC}$即可,根据平行四边形的对边平行且相等可得$\overrightarrow{AD}$=$\overrightarrow{BC}$,然后根据向量的三角形法则求解即可;
(2)根据平行四边形的对边平行且相等可得$\overrightarrow{DC}$=$\overrightarrow{AB}$,然后根据向量的平行四边形法则作出以DC、DE为邻边的平行四边形,其对角线即为所求.
解答 解:(1)$\overrightarrow{DA}$+$\overrightarrow{DC}$=$\overrightarrow{DB}$,
∵$\overrightarrow{AD}$=$\overrightarrow{BC}$,
∴$\overrightarrow{AE}$-$\overrightarrow{BC}$=$\overrightarrow{AE}$-$\overrightarrow{AD}$=$\overrightarrow{DE}$;
故答案为:$\overrightarrow{DB}$;$\overrightarrow{DE}$.
(2)如图,$\overrightarrow{DF}$即为所求$\overrightarrow{AB}$+$\overrightarrow{DE}$.
点评 本题考查了平面向量,平行四边形的性质,向量的问题,熟练掌握平行四边形法则和三角形法则是解题的关键.

练习册系列答案
相关题目
10.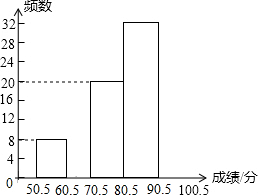 某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:
某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:
(1)求a的值,并补全频数分布直方图.
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
 某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:
某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:| 分组 | 频数 | 频率 |
| 50.5-60.5 | 8 | 0.08 |
| 60.5-70.5 | 12 | 0.12 |
| 70.5-80.5 | 20 | 0.2 |
| 80.5-90.5 | 32 | 0.32 |
| 90.5-100.5 | 28 | a |
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
11.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
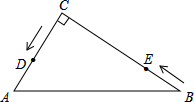 如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C→A→B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为ts(0<t<8).
如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C→A→B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为ts(0<t<8). 如图,在矩形ABCD中,AB=4,BC=8,Rt△EFG中,EF=4,EG=3,∠GEF=90°,与点B与点E重合时,将△EFG绕点E顺时针旋转α(0°<α<90°),直线FG分别与直线AD、BD相交于M、N,当△DMN是直角三角形时,线段MN的值是2$\sqrt{5}$-$\frac{6}{5}$或$\frac{14}{5}$.
如图,在矩形ABCD中,AB=4,BC=8,Rt△EFG中,EF=4,EG=3,∠GEF=90°,与点B与点E重合时,将△EFG绕点E顺时针旋转α(0°<α<90°),直线FG分别与直线AD、BD相交于M、N,当△DMN是直角三角形时,线段MN的值是2$\sqrt{5}$-$\frac{6}{5}$或$\frac{14}{5}$.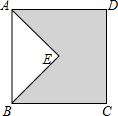 如图,四边形ABCD是正方形,AE垂直于BE,AE=3,BE=4,则图中阴影部分的面积是19.
如图,四边形ABCD是正方形,AE垂直于BE,AE=3,BE=4,则图中阴影部分的面积是19. 在平面直角坐标系中,A,B,C三点的坐标分别为(-5,4),(-3,0),(0,2).
在平面直角坐标系中,A,B,C三点的坐标分别为(-5,4),(-3,0),(0,2).