题目内容
9.如果直角三角形两直角边为5:12,则斜边上的高与斜边的比为( )| A. | 60:13 | B. | 5:12 | C. | 12:13 | D. | 60:169 |
分析 可在直角三角形中,用勾股定理求出斜边的长,然后根据三角形面积的不同表示方法,求出斜边上的高.进而可得出斜边与斜边上的高的比例关系.
解答 解:如图,在Rt△ABC中,∠ACB=90°,AC=5k,BC=12k,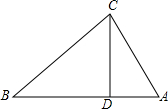
根据勾股定理有:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13k,
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
∴CD=$\frac{AC•BC}{AB}$=$\frac{60}{13}$,
∴AB:CD=13:$\frac{60}{13}$=169:60,
即斜边上的高与斜边的比=60:169,
故选D.
点评 本题考查了勾股定理得运用,能够根据已知条件结合勾股定理求出直角三角形的三边.特别注意结论:直角三角形斜边上的高等于两条直角边的乘积除以斜边.此结论在计算中运用可以简便计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.如果a2n-1•an+2=a7,则n的值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
18.若a>b,则下列式子中错误的是( )
| A. | a-5>b-5 | B. | 5-a>5-b | C. | 5a>5b | D. | $\frac{a}{5}$>$\frac{b}{5}$ |
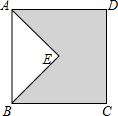 如图,四边形ABCD是正方形,AE垂直于BE,AE=3,BE=4,则图中阴影部分的面积是19.
如图,四边形ABCD是正方形,AE垂直于BE,AE=3,BE=4,则图中阴影部分的面积是19.