题目内容
17.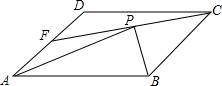 在平行四边形ABCD中,F是AD的中点,BP⊥CF交于点P,若AP=2$\sqrt{3}$,求AB的长.
在平行四边形ABCD中,F是AD的中点,BP⊥CF交于点P,若AP=2$\sqrt{3}$,求AB的长.
分析 延长BA与CF的延长线交于点E,证明△AEF≌△DCF,而后运用直角三角形斜边中线等于斜边一半即可求解.
解答 解:如图1,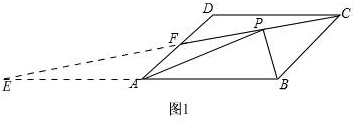
延长BA与CF的延长线交于点E,
∵平行四边形ABCD,
∴AB=CD,AB∥CD,
∴∠E=∠DCF,∠EAF=∠CDF,
∵F为AD的中点,
∴AF=DF,
在△AEF和△DCF中,
$\left\{\begin{array}{l}{∠E=∠DCF}\\{∠EAF=∠CDF}\\{AF=DF}\end{array}\right.$,
∴△AEF≌△DCF (AAS),
∴AE=CD,
∴AB=AE,
∴A是BE的中点,
∵BP⊥CF,
∴在直角△BPE中,
∴AP=AB=AE,
∵AP=$2\sqrt{3}$,
∴AB=$2\sqrt{3}$.
点评 此题主要考查平行四边形的性质,熟悉平行四边形性质会构造全等三角形运用直角三角形斜边中线等于斜边一半是解题的关键.

练习册系列答案
相关题目
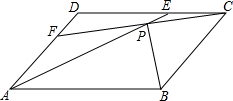 在?ABCD的两边AD,CD上各取一点F,E,连接AE,CF交于点P,且AE=CF.求证:PB平分∠APC.
在?ABCD的两边AD,CD上各取一点F,E,连接AE,CF交于点P,且AE=CF.求证:PB平分∠APC.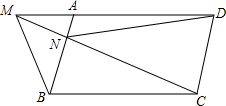 已知M是?ABCD的DA边的延长线上任一点,连结MC交AB于N,求证:S△MNB=S△AND.
已知M是?ABCD的DA边的延长线上任一点,连结MC交AB于N,求证:S△MNB=S△AND.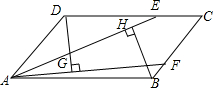 如图,在平行四边形ABCD中,点E,F分别在BC,CD上,且AE=AF,DG⊥AE,BH⊥AF,点G,H为垂足,猜想DG与BH的大小关系,并证明你的猜想.
如图,在平行四边形ABCD中,点E,F分别在BC,CD上,且AE=AF,DG⊥AE,BH⊥AF,点G,H为垂足,猜想DG与BH的大小关系,并证明你的猜想.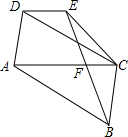 如图,在?ABCD中,过点B作BE交对角线AC于点F,且BF=EF,连接DE、CE,求证:AC∥DE.
如图,在?ABCD中,过点B作BE交对角线AC于点F,且BF=EF,连接DE、CE,求证:AC∥DE.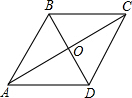 如图,菱形ABCD的周长为20cm,对角线AC、BD相交于点O,AC=8cm,求对角线BD的长和菱形ABCD的面积.
如图,菱形ABCD的周长为20cm,对角线AC、BD相交于点O,AC=8cm,求对角线BD的长和菱形ABCD的面积. 八年级(3)班同学要在广场上布置一个矩形的花坛,计划用红花摆成两条对角线,如果一条对角线用了38盆红花,还需要从花房运来多少盆红花?为什么?如果一条对角线用了49盆呢?
八年级(3)班同学要在广场上布置一个矩形的花坛,计划用红花摆成两条对角线,如果一条对角线用了38盆红花,还需要从花房运来多少盆红花?为什么?如果一条对角线用了49盆呢?