题目内容
10. 已知,如图,四边形ABEG、GEFH、HFCD都是边长为a的正方形,求证:∠AFB+∠ACB=45°.
已知,如图,四边形ABEG、GEFH、HFCD都是边长为a的正方形,求证:∠AFB+∠ACB=45°.
分析 由正方形的性质得出∠AEB=45°,AB=BE=EF=FC=a,∠B=90°,EC=2a,由勾股定理求出AE=$\sqrt{2}$a,证出$\frac{AE}{EF}=\frac{EC}{AE}$,再由公共角∠AEF=∠CEA,得出△AEF∽△CEA,得出对应角相等∠AFB=∠EAC,再由三角形的外角性质即可得出结论.
解答 解:∵四边形ABEG、GEFH、HFCD都是边长为a的正方形,
∴∠AEB=45°,AB=BE=EF=FC=a,∠B=90°,
∴EC=2a,AE=$\sqrt{{a}^{2}+{a}^{2}}$=$\sqrt{2}$a,
∵$\frac{AE}{EF}=\frac{\sqrt{2}a}{a}$=$\sqrt{2}$,$\frac{EC}{AE}=\frac{2a}{\sqrt{2}a}$=$\sqrt{2}$,
∴$\frac{AE}{EF}=\frac{EC}{AE}$,
又∵∠AEF=∠CEA,
∴△AEF∽△CEA,
∴∠AFB=∠EAC,
∵∠AEB=∠EAC+∠ACB=45°,
∴∠AFB+∠ACB=45°.
点评 本题考查了正方形的性质、相似三角形的判定与性质;熟练掌握相似三角形的判定与性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
5.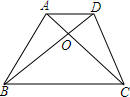 如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,且AD:BC=1:2,则下列结论中,错误的是( )
如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,且AD:BC=1:2,则下列结论中,错误的是( )
 如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,且AD:BC=1:2,则下列结论中,错误的是( )
如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,且AD:BC=1:2,则下列结论中,错误的是( )| A. | S△ABC=S△DBC | B. | S△AOB=S△COD | C. | 2S△AOD=S△BOC | D. | 2S△AOB=S△BOC |

 如图,四边形ABCD是平行四边形,点E为DC延长线上一点,联接AE,交边BC于点F,联接BE.求证:AB•AD=BF•ED.
如图,四边形ABCD是平行四边形,点E为DC延长线上一点,联接AE,交边BC于点F,联接BE.求证:AB•AD=BF•ED.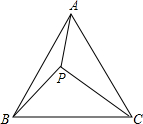 数学探究课上老师处这样一道题:“如图,等边△ABC中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军探讨时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断
数学探究课上老师处这样一道题:“如图,等边△ABC中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军探讨时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断 小华想知道线段AB和DF是否平行,但是他只带了一个三角板,于是他想了这样一个办法.
小华想知道线段AB和DF是否平行,但是他只带了一个三角板,于是他想了这样一个办法.