题目内容
 如图,四边形ABCD中,∠ABC=90°,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F,DF=BC.求证:ED-FC=BE.
如图,四边形ABCD中,∠ABC=90°,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F,DF=BC.求证:ED-FC=BE.考点:全等三角形的判定与性质
专题:证明题
分析:延长EB至G,使BG=CF,连接CG,证△BCG≌△FDC,推出CD=CG,∠1=∠2,求出∠DCE=∠ECG,证△DEC≌△EGC,推出ED=EG即可.
解答:证明:延长EB至G,使BG=CF,连接CG,
∵DF⊥BC,
∴∠CBG=∠DFC=90°,
在△BCG和△FDC中
∴△BCG≌△FDC,
∴CD=CG,∠1=∠2,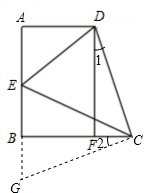
∵∠1+∠DCF=90°,
∴∠2+∠DCF=90°,
∵∠DCE=45°,
∴∠ECG=45°,
∴∠DCE=∠ECG,
在△DEC和△EGC中,
∴△DEC≌△EGC(SAS),
∴ED=EG,
∴ED-FC=BE.
∵DF⊥BC,
∴∠CBG=∠DFC=90°,
在△BCG和△FDC中
|
∴△BCG≌△FDC,
∴CD=CG,∠1=∠2,

∵∠1+∠DCF=90°,
∴∠2+∠DCF=90°,
∵∠DCE=45°,
∴∠ECG=45°,
∴∠DCE=∠ECG,
在△DEC和△EGC中,
|
∴△DEC≌△EGC(SAS),
∴ED=EG,
∴ED-FC=BE.
点评:本题主要考查对三角形内角和定理,全等三角形的性质和判定等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.

练习册系列答案
相关题目
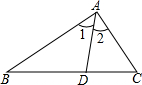 如图,∠1=∠2,∠C=2∠B,求证:AB=AC+CD.
如图,∠1=∠2,∠C=2∠B,求证:AB=AC+CD.