题目内容
若点P在正方形ABCD内,且AP=5,BP=4,PC=1,则正方形ABCD的面积为 .
考点:正方形的性质,勾股定理
专题:
分析:由题意得出PA2+PC2=PB2+PD2,解得PD,进一步作PH、PI、PJ、PK垂直于AB、BC、CD、DA于点H、I、J、K.利用正方形的性质,设出正方形的边长为a,PH=x,PI=y,进一步由勾股定理求得答案即可.
解答:解:如图,

由已知可得:PA2+PC2=PB2+PD2,
则PD=
,
分别作PH、PI、PJ、PK垂直于AB、BC、CD、DA于点H、I、J、K.
设正方形的边长为a,PH=x,PI=y,PJ=a-x,PK=a-y.
PH2+PK2=PA2,
PH2+PI2=PB2,
PI2+PJ2=PC2,
PJ2+PK2=PD2,
即x2+(a-y)2=25,①
x2+y2=16,②
y2+(a-x)2=1,③
(a-x)2+(a-y)2=10,④
解①②③④组成方程组得到:a-2ay=9,y=
,a-2ax=15,x=
,
再代入②得,a4-26a2+153=0,
解得a2=9或a2=17.
即正方形的面积为9或17.
故答案为:9或17.

由已知可得:PA2+PC2=PB2+PD2,
则PD=
| 10 |
分别作PH、PI、PJ、PK垂直于AB、BC、CD、DA于点H、I、J、K.
设正方形的边长为a,PH=x,PI=y,PJ=a-x,PK=a-y.
PH2+PK2=PA2,
PH2+PI2=PB2,
PI2+PJ2=PC2,
PJ2+PK2=PD2,
即x2+(a-y)2=25,①
x2+y2=16,②
y2+(a-x)2=1,③
(a-x)2+(a-y)2=10,④
解①②③④组成方程组得到:a-2ay=9,y=
| a2-9 |
| 2a |
| a2+15 |
| 2a |
再代入②得,a4-26a2+153=0,
解得a2=9或a2=17.
即正方形的面积为9或17.
故答案为:9或17.
点评:此题考查正方形的性质,勾股定理的运用,注意利用题目中的条件,画出图形,作出辅助线解决问题.

练习册系列答案
相关题目
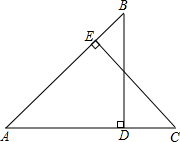 如图,BD⊥AC,CE⊥AB,垂足分别为D、E,AD=AE.下列方法中,可以直接判断△ADB≌△AEC的是( )
如图,BD⊥AC,CE⊥AB,垂足分别为D、E,AD=AE.下列方法中,可以直接判断△ADB≌△AEC的是( )| A、SSS | B、SAS |
| C、ASA | D、AAS |
 如图,四边形ABCD中,∠ABC=90°,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F,DF=BC.求证:ED-FC=BE.
如图,四边形ABCD中,∠ABC=90°,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F,DF=BC.求证:ED-FC=BE. 反比例函数y=
反比例函数y=


