题目内容
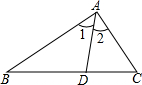 如图,∠1=∠2,∠C=2∠B,求证:AB=AC+CD.
如图,∠1=∠2,∠C=2∠B,求证:AB=AC+CD.考点:全等三角形的判定与性质
专题:证明题
分析:在AB上取点E,使得AE=AC,则可证得△AED≌△ACD,可得∠AED=∠C=2∠B,ED=CD,可证得△BDE为等腰三角形,所以有BE=DE=CD,可得结论.
解答:
证明:
在AB上取点E,使得AE=AC,
在△AED和△ACD中
∴△AED≌△ACD,
∴∠AED=∠C,AE=AC,ED=CD,
∵∠C=2∠B,且∠AED=∠B+∠BDE
∴∠B=∠BDE,
∴BD=DE,
∴AB=AE+BD=AC+DE=AC+CD.

证明:
在AB上取点E,使得AE=AC,
在△AED和△ACD中
|
∴△AED≌△ACD,
∴∠AED=∠C,AE=AC,ED=CD,
∵∠C=2∠B,且∠AED=∠B+∠BDE
∴∠B=∠BDE,
∴BD=DE,
∴AB=AE+BD=AC+DE=AC+CD.
点评:本题主要考查三角形全等的判定和性质,解题的关键是构造全等三角形.

练习册系列答案
相关题目
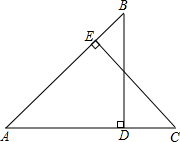 如图,BD⊥AC,CE⊥AB,垂足分别为D、E,AD=AE.下列方法中,可以直接判断△ADB≌△AEC的是( )
如图,BD⊥AC,CE⊥AB,垂足分别为D、E,AD=AE.下列方法中,可以直接判断△ADB≌△AEC的是( )| A、SSS | B、SAS |
| C、ASA | D、AAS |
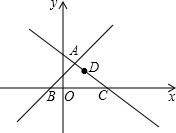 如图,在平面直角坐标系xOy中,直线y=x+1与y=-
如图,在平面直角坐标系xOy中,直线y=x+1与y=- 已知如图AB=AC,∠BAO=∠CAO,求证:∠OBC=∠OCB.
已知如图AB=AC,∠BAO=∠CAO,求证:∠OBC=∠OCB. 如图,四边形ABCD中,∠ABC=90°,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F,DF=BC.求证:ED-FC=BE.
如图,四边形ABCD中,∠ABC=90°,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F,DF=BC.求证:ED-FC=BE.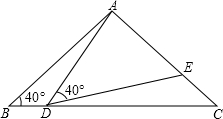 如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.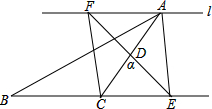 如图,在△ABC中∠ACB=90°,D是AC的中点,过点A的直线l∥BC,将直线AC绕点D逆时针旋转(旋转角α<∠ACB),分别交直线l于点F与BC的延长线交于点E,连接AE、CF.
如图,在△ABC中∠ACB=90°,D是AC的中点,过点A的直线l∥BC,将直线AC绕点D逆时针旋转(旋转角α<∠ACB),分别交直线l于点F与BC的延长线交于点E,连接AE、CF.