题目内容
某宾馆有120间标准房，当标准房价格为100元时，每天都客满，市场调查表明单间房价在100～150元之间（含100元，150元）浮动时，每提高10元，日均入住数减少6间，如果不考虑其他因素，宾馆将标准房价格提高到多少元时，客房的日营业额最大？
考点：二次函数的应用
专题：
分析：首先设宾馆客房租金每间日租金提高x个10元，以及客房租金总收入为y．，建立y与x的关系式，并通过二次函数求解最大值．
解答：解：设宾馆客房租金每间日租金提高x个10元，
将有6x间客房空出，客房租金总收入为y．
由题意可得：
y=（100+10x）（120-6x）（10≤x≤50且x是整数）．
=60（-x2+10x+200）
=-60（x-5）2+13500
当x=5时，ymax=13500．
因此每间租金100+10×5=150元时，客房租金总收入最高，日租金13500元．
将有6x间客房空出，客房租金总收入为y．
由题意可得：
y=（100+10x）（120-6x）（10≤x≤50且x是整数）．
=60（-x2+10x+200）
=-60（x-5）2+13500
当x=5时，ymax=13500．
因此每间租金100+10×5=150元时，客房租金总收入最高，日租金13500元．
点评：本题考查根据实际问题选择函数类型，通过实际问题，抽象出函数模型，并通二次函数计算最大值，考查对知识的综合运用能力，属于中档题．
练习册系列答案
相关题目
已知反比例函数y=
的图象在每一个象限内，y随x的增大而减小，则（ ）
| 5-m |
| x |
| A、m≥5 | B、m＜5 |
| C、m＞5 | D、m≤5 |
如图，四边形ABCD中，∠ABC=90°，点E是AB上的点，∠ECD=45°，连接ED，过D作DF⊥BC于F，DF=BC．求证：ED-FC=BE．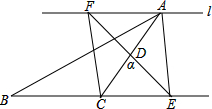
如图，在△ABC中∠ACB=90°，D是AC的中点，过点A的直线l∥BC，将直线AC绕点D逆时针旋转（旋转角α＜∠ACB），分别交直线l于点F与BC的延长线交于点E，连接AE、CF．