题目内容
20．
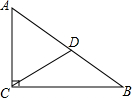在△ABC中，∠BCA=90°，∠B=30°，AB=5cm，CD为斜边AB的中线，以点D为圆心，DC长为半径画⊙D，试说明点A、B、C与⊙D的位置关系．
分析 根据直角三角形斜边上的中线等于斜边的一半判断DA、DB与DC的数量关系，根据点与圆的位置关系的判断方法进行判断即可．
解答 解：∵∠BCA=90°，CD为斜边AB的中线，
∴DA=DB=DC，
∴点A、B、C都在以点D为圆心，DC长为半径画⊙D上．
点评 本题考查了对点与圆的位置关系的判断．关键要记住若半径为r，点到圆心的距离为d，则有：当d＞r时，点在圆外；当d=r时，点在圆上，当d＜r时，点在圆内．
练习册系列答案
相关题目
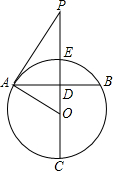如图，过圆心O的直线PC垂直弦AB于点D，并且与⊙O交于C、E两点．
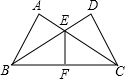如图，∠A=∠D=90°，AB=DC，AC与BD相交于点E，F是BC的中点．下列说法：①BE=EC；②BF=FC；③EF⊥BC；④∠BEF=∠CEF，正确的有（ ）个．
如图，在△ABC中，∠ABC=2∠C，点E为AC的中点，AD⊥BC于点D，ED延长后交AB延长线于点F，求证：△AEF∽△ABC．
已知：如图，AB∥CD，求证：∠BED=∠D-∠B．