题目内容
10.计算:$\frac{1}{x}$-$\frac{1}{x(x+1)}$-$\frac{1}{(x+1)(x+2)}$-…-$\frac{1}{(x+2015)(x+2016)}$.分析 原式利用拆项法变形,抵消合并即可得到结果.
解答 解:原式=$\frac{1}{x}$-($\frac{1}{x}$-$\frac{1}{x+1}$)-($\frac{1}{x+1}$-$\frac{1}{x+2}$)-…-($\frac{1}{x+2015}$-$\frac{1}{x+2016}$)=$\frac{1}{x}$-$\frac{1}{x}$+$\frac{1}{x+1}$-$\frac{1}{x+1}$+$\frac{1}{x+2}$-…-$\frac{1}{x+2015}$+$\frac{1}{x+2016}$=$\frac{1}{x+2016}$.
点评 此题考查了分式的加减法,熟练掌握拆项的方法是解本题的关键.

练习册系列答案
相关题目
 如图所示,直径为10的圆A经过点C(0,5)和点O (0,0),B是y轴右侧圆A优弧上一点,那么sin∠OBC的值是$\frac{1}{2}$.
如图所示,直径为10的圆A经过点C(0,5)和点O (0,0),B是y轴右侧圆A优弧上一点,那么sin∠OBC的值是$\frac{1}{2}$.
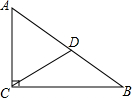 在△ABC中,∠BCA=90°,∠B=30°,AB=5cm,CD为斜边AB的中线,以点D为圆心,DC长为半径画⊙D,试说明点A、B、C与⊙D的位置关系.
在△ABC中,∠BCA=90°,∠B=30°,AB=5cm,CD为斜边AB的中线,以点D为圆心,DC长为半径画⊙D,试说明点A、B、C与⊙D的位置关系.