题目内容
11.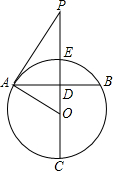 如图,过圆心O的直线PC垂直弦AB于点D,并且与⊙O交于C、E两点.
如图,过圆心O的直线PC垂直弦AB于点D,并且与⊙O交于C、E两点.(1)若sin∠DAO=$\frac{2}{3}$且OE=2PE,求证:AP是⊙O的切线.
(2)若D是OE的中点,AB=4,求CE.
分析 (1)通过证得△AOD∽△POA,从而证得∠PAO=∠ADO=90°,即可证得结论;
(2)根据垂径定理和勾股定理即可求得半径,根据半径求得直径即可.
解答 (1)证明:∵sin∠DAO=$\frac{2}{3}$,OD⊥AB,
∴$\frac{OD}{OA}$=$\frac{2}{3}$,
∵OE=2PE,
∴$\frac{OE}{OP}$=$\frac{2}{3}$
∵OA=OE,
∴$\frac{OA}{OP}$=$\frac{OD}{OA}$=$\frac{2}{3}$,
∵∠AOD=∠POA,
∴△AOD∽△POA,
∴∠PAO=∠ADO=90°,
∴AP是⊙O的切线.
(2)解:设OA=OE=x,
∵D是OE的中点,
∴OD=$\frac{1}{2}$x,
∵AB=2,OD⊥AB,
∴AD=1,
在RT△AOD中,OA2=OD2+AD2,
即x2=($\frac{1}{2}$x)2+12,解得x=$\frac{2}{3}$$\sqrt{3}$,
∴CE=2OE=2×$\frac{2}{3}$$\sqrt{3}$=$\frac{4}{3}$$\sqrt{3}$.
点评 本题考查了垂径定理和勾股定理的应用,三角形相似的判定和性质,切线的判定等,熟练掌握性质定理是解题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 如图,已知AD⊥AB,AC⊥AE,且AD=AB,AC=AE,请判断BE和CD的关系并证明.
如图,已知AD⊥AB,AC⊥AE,且AD=AB,AC=AE,请判断BE和CD的关系并证明.
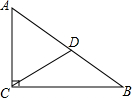 在△ABC中,∠BCA=90°,∠B=30°,AB=5cm,CD为斜边AB的中线,以点D为圆心,DC长为半径画⊙D,试说明点A、B、C与⊙D的位置关系.
在△ABC中,∠BCA=90°,∠B=30°,AB=5cm,CD为斜边AB的中线,以点D为圆心,DC长为半径画⊙D,试说明点A、B、C与⊙D的位置关系. 若表示m、n两个实数的点在数轴上的位置如图所示,则化简$\sqrt{(m+n)^{2}}$+|m-n|的结果为-2n.
若表示m、n两个实数的点在数轴上的位置如图所示,则化简$\sqrt{(m+n)^{2}}$+|m-n|的结果为-2n.