题目内容
5. 如图,在△ABC中,∠ABC=2∠C,点E为AC的中点,AD⊥BC于点D,ED延长后交AB延长线于点F,求证:△AEF∽△ABC.
如图,在△ABC中,∠ABC=2∠C,点E为AC的中点,AD⊥BC于点D,ED延长后交AB延长线于点F,求证:△AEF∽△ABC.
分析 先根据直角三角形斜边上的中线性质得到ED=EC,则∠EDC=∠C,再利用三角形外角性质可得∠AEF=2∠C,而∠ABC=2∠C,所以∠ABC=∠AEF,加上∠EAF=∠BAC,则根据有两组角对应相等的两个三角形相似可判断△AEF∽△ABC.
解答 证明:∵AD⊥BC,
∴∠ADC=90°,
∴点E为AC的中点,
∴ED=EC,
∴∠EDC=∠C,
∴∠AEF=∠EDC+∠C=2∠C,
∵∠ABC=2∠C,
∴∠ABC=∠AEF,
∵∠EAF=∠BAC,
∴△AEF∽△ABC.
点评 本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了直角三角形斜边上的中线性质.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
14.有四张不透明的卡片,正面分别标有数字3、$\frac{25}{9}$、$\sqrt{3}$、π.除正面的数字不同外,其余都相同.将它们背面朝上洗匀后,从中随机抽取一张,抽到写有无理数卡片的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
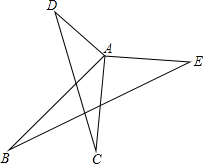 如图,已知AD⊥AB,AC⊥AE,且AD=AB,AC=AE,请判断BE和CD的关系并证明.
如图,已知AD⊥AB,AC⊥AE,且AD=AB,AC=AE,请判断BE和CD的关系并证明.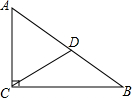 在△ABC中,∠BCA=90°,∠B=30°,AB=5cm,CD为斜边AB的中线,以点D为圆心,DC长为半径画⊙D,试说明点A、B、C与⊙D的位置关系.
在△ABC中,∠BCA=90°,∠B=30°,AB=5cm,CD为斜边AB的中线,以点D为圆心,DC长为半径画⊙D,试说明点A、B、C与⊙D的位置关系.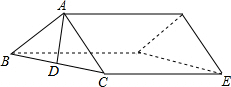 在我国南方农村,常见到如图的屋顶,为防雨需在房顶铺上油毡,已知AB=AC,AD为△ABC的中线,且AD=3m,BC=8m,CE=10m,问需要用油毡多少平方米?
在我国南方农村,常见到如图的屋顶,为防雨需在房顶铺上油毡,已知AB=AC,AD为△ABC的中线,且AD=3m,BC=8m,CE=10m,问需要用油毡多少平方米?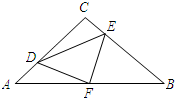 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF
如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF