题目内容
19.已知a、b、c均为正数,且k=$\frac{a}{b+c}$=$\frac{b}{a+c}$=$\frac{c}{a+b}$,在下列四个点中,正比例函数y=kx的图象一定经过的点的坐标是( )| A. | (1,$\frac{1}{2}$) | B. | (1,2) | C. | (1,-$\frac{1}{2}$) | D. | (1,-1) |
分析 由k=$\frac{a}{b+c}$=$\frac{b}{a+c}$=$\frac{c}{a+b}$得出a=k(b+c)①,b=k(a+c)②,c=k(a+b)③,①+②+③得2k=1,则求得k=$\frac{1}{2}$,然后把A、B、C、D的坐标分别代入解析式即可判定.
解答 解:∵a、b、c均为正数,且k=$\frac{a}{b+c}$=$\frac{b}{a+c}$=$\frac{c}{a+b}$,
∴a=k(b+c)①
b=k(a+c)②
c=k(a+b)③
①+②+③得2k=1,则k=$\frac{1}{2}$,
∴正比例函数为y=$\frac{1}{2}$x,
把A、B、C、D的坐标分别代入解析式,则(1,$\frac{1}{2}$)符合解析式.
故选A.
点评 本题考查了一次函数图象上点的坐标特征,根据已知条件求得k的值是解题的关键.

练习册系列答案
相关题目
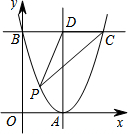 如图,在平面直角坐标系中,抛物线y=(x-2)2与x轴交于点A,与y轴交于点B.过点B作BC∥x轴,交抛物线于点C,过点A作AD∥y轴,交BC于点D,点P在BC下方的抛物线上(P不与B,C重合),连结PC,PD,则△PCD面积的最大值是4.
如图,在平面直角坐标系中,抛物线y=(x-2)2与x轴交于点A,与y轴交于点B.过点B作BC∥x轴,交抛物线于点C,过点A作AD∥y轴,交BC于点D,点P在BC下方的抛物线上(P不与B,C重合),连结PC,PD,则△PCD面积的最大值是4.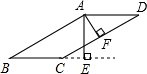 如图,四边形ABCD是平行四边形,AE⊥BC交BC的延长线与E,AF⊥CD交CD于F,且∠EAF=30°,AE=4,AF=3.求:
如图,四边形ABCD是平行四边形,AE⊥BC交BC的延长线与E,AF⊥CD交CD于F,且∠EAF=30°,AE=4,AF=3.求: