题目内容
8.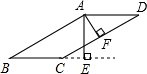 如图,四边形ABCD是平行四边形,AE⊥BC交BC的延长线与E,AF⊥CD交CD于F,且∠EAF=30°,AE=4,AF=3.求:
如图,四边形ABCD是平行四边形,AE⊥BC交BC的延长线与E,AF⊥CD交CD于F,且∠EAF=30°,AE=4,AF=3.求:(1)?ABCD的周长;
(2)?ABCD的面积.
分析 (1)由?ABCD中,AE⊥BC交BC延长线于E,AF⊥DC于F,∠EAF=30°,易求得∠B=∠D=30°,然后由含30°角的直角三角形的性质,求得AD与AB的长,则可求得?ABCD的周长.
(2)由(1)可得BC的长,利用平行四边形的面积公式即可求出其面积.
解答 解:(1)∵AE⊥BC,AF⊥DC,
∴∠AFD=∠AEB=90°,
∵四边形ABCD是平行四边形,
∴∠B=∠D,AD∥BC,
∴∠DAE=∠AEB=90°,
∵∠EAF=30°,
∴∠DAF=90°-∠EAF=60°,
∴∠D=90°-∠DAF=30°,
∴∠B=∠D=30°,
∵AE=4厘米,AF=3厘米,
在Rt△ABE中,AB=2AE=8厘米,
在Rt△ADF中,AD=2AF=6厘米,
∴?ABCD的周长为:2(AB+AD)=28(厘米).
(2)∵AD=BC=6cm,AE=4cm,
∴?ABCD的面积=24cm2.
点评 此题考查了平行四边形的性质以及含30°角的直角三角形的性质.此题难度适中,解题的关键是求出AB和AD的长.

练习册系列答案
相关题目
19.已知a、b、c均为正数,且k=$\frac{a}{b+c}$=$\frac{b}{a+c}$=$\frac{c}{a+b}$,在下列四个点中,正比例函数y=kx的图象一定经过的点的坐标是( )
| A. | (1,$\frac{1}{2}$) | B. | (1,2) | C. | (1,-$\frac{1}{2}$) | D. | (1,-1) |
10.下列事件中是必然事件的是( )
| A. | 抛掷一枚质地均匀的硬币,落地后正面朝上 | |
| B. | 营山县8月份某一天的最低气温是-20℃ | |
| C. | 通常加热到100℃时,水沸腾 | |
| D. | 打开电视,正在播放节目《新闻联播》 |
 如图,△ABC中,AB=AC,点D、E分别在AB、AC边上,∠EBC=∠DCB
如图,△ABC中,AB=AC,点D、E分别在AB、AC边上,∠EBC=∠DCB