题目内容
10．若x-$\frac{1}{x}$=5，则x2+$\frac{1}{{x}^{2}}$=27，（x+$\frac{1}{x}$）2=29．分析 将x-$\frac{1}{x}$=5两边平方，再化简整理解答即可．
解答 解：将x-$\frac{1}{x}$=5平方，可得：x2-2+$\frac{1}{{x}^{2}}$=25，
解得：x2+$\frac{1}{{x}^{2}}$=27，
（x+$\frac{1}{x}$）2=x2+2+$\frac{1}{{x}^{2}}$=2+27=29．
故答案为：27；29．
点评 此题考查完全平方公式，关键是把x-$\frac{1}{x}$=5两边平方整理化简．
练习册系列答案
相关题目
20．下列运算正确的是（ ）
| A． | a2+a2=a4 | B． | （x3）2=x5 | C． | （a-b）2=a2-b2 | D． | $\root{3}{-27}=-3$ |
1．
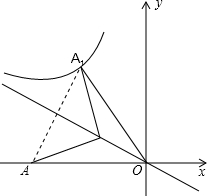如图，在平面直角坐标系中，A（-10，0），点B在第二象限，tan∠AOB=$\frac{1}{2}$，点A和点A1关于直线OB对称，且A1在双曲线y=$\frac{k}{x}$（k≠0）上，则k的值（ ）
如图，在平面直角坐标系中，A（-10，0），点B在第二象限，tan∠AOB=$\frac{1}{2}$，点A和点A1关于直线OB对称，且A1在双曲线y=$\frac{k}{x}$（k≠0）上，则k的值（ ）| A． | -12 | B． | -12$\sqrt{5}$ | C． | -24 | D． | -48 |
如图，△ABC中，AB=AC，点D、E分别在AB、AC边上，∠EBC=∠DCB
（1）如图，在△ABC中，AD⊥BC，∠1=∠B，求证：△ABC是直角三角形．
2．
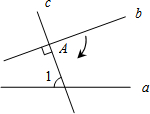如图，直线a与直线b被直线c所截，b⊥c，垂足为点A，∠1=70°．若使直线b与直线a平行，则可将直线b绕着点A顺时针旋转（ ）
如图，直线a与直线b被直线c所截，b⊥c，垂足为点A，∠1=70°．若使直线b与直线a平行，则可将直线b绕着点A顺时针旋转（ ）| A． | 70° | B． | 50° | C． | 30° | D． | 20° |
19．已知a、b、c均为正数，且k=$\frac{a}{b+c}$=$\frac{b}{a+c}$=$\frac{c}{a+b}$，在下列四个点中，正比例函数y=kx的图象一定经过的点的坐标是（ ）
| A． | （1，$\frac{1}{2}$） | B． | （1，2） | C． | （1，-$\frac{1}{2}$） | D． | （1，-1） |