题目内容
9.已知在△ABC中,AB=AC=2$\sqrt{10}$,BC=4.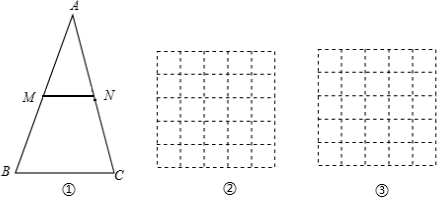
(1)如图,M是AB的中点,在AC边上取一点N,使得△AMN与△ABC相似,求线段MN的长.
(2)图②和图③分别是由20个边长为1的正方形组成的5×4的网格,请在图②和图③中各画一个△A′B′C′,使得它们同时满足以下条件:①△A′B′C′的三个顶点都是网格内正方形的顶点;②△A′B′C′∽△ABC;③所画的两个三角形与△AMN和△ABC都互不全等.
分析 (1)利用相似三角形的判定与性质进而求出即可;
(2)可以利用两三角形相似比为2:1,进而画出即可.
解答 解:(1)∵在△ABC中,AB=AC=2$\sqrt{10}$,M是AB的中点,在AC边上取一点N,使得△AMN与△ABC相似,
∴只有当MN∥BC时,△AMN∽△ABC,
故$\frac{AM}{AB}$=$\frac{AN}{AC}$=$\frac{MN}{BC}$,
则$\frac{1}{2}$=$\frac{MN}{4}$,
解得:MN=2;
(2)如图所示: .
.
点评 此题主要考查了相似变换以及相似三角形的判定与性质,注意相似三角形的性质是解题关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
20.下列运算正确的是( )
| A. | a2+a2=a4 | B. | (x3)2=x5 | C. | (a-b)2=a2-b2 | D. | $\root{3}{-27}=-3$ |
4. 如图,⊙O中,半径OC=4,弦AB垂直平分OC,则AB的长是( )
如图,⊙O中,半径OC=4,弦AB垂直平分OC,则AB的长是( )
 如图,⊙O中,半径OC=4,弦AB垂直平分OC,则AB的长是( )
如图,⊙O中,半径OC=4,弦AB垂直平分OC,则AB的长是( )| A. | 3 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
1.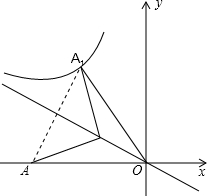 如图,在平面直角坐标系中,A(-10,0),点B在第二象限,tan∠AOB=$\frac{1}{2}$,点A和点A1关于直线OB对称,且A1在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值( )
如图,在平面直角坐标系中,A(-10,0),点B在第二象限,tan∠AOB=$\frac{1}{2}$,点A和点A1关于直线OB对称,且A1在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值( )
 如图,在平面直角坐标系中,A(-10,0),点B在第二象限,tan∠AOB=$\frac{1}{2}$,点A和点A1关于直线OB对称,且A1在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值( )
如图,在平面直角坐标系中,A(-10,0),点B在第二象限,tan∠AOB=$\frac{1}{2}$,点A和点A1关于直线OB对称,且A1在双曲线y=$\frac{k}{x}$(k≠0)上,则k的值( )| A. | -12 | B. | -12$\sqrt{5}$ | C. | -24 | D. | -48 |
19.已知a、b、c均为正数,且k=$\frac{a}{b+c}$=$\frac{b}{a+c}$=$\frac{c}{a+b}$,在下列四个点中,正比例函数y=kx的图象一定经过的点的坐标是( )
| A. | (1,$\frac{1}{2}$) | B. | (1,2) | C. | (1,-$\frac{1}{2}$) | D. | (1,-1) |
 已知关于x的一元二次方程x2-(3m+2)x+(2m2+2m-$\frac{1}{2}$)=0.
已知关于x的一元二次方程x2-(3m+2)x+(2m2+2m-$\frac{1}{2}$)=0.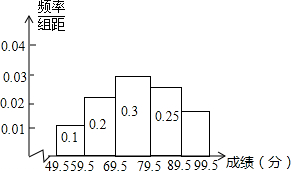 某区有6000名学生参加了“创建国家卫生城市”知识竞赛,为了了解本次竞赛成绩分布情况,竞赛组委会从中随机抽取部分学生的成绩(得分都是整数)作为样本,绘制成频率分布直方图如图,请根据提供的信息估计该区本次竞赛成绩在89.5分-99.5分的学生大约有900名.
某区有6000名学生参加了“创建国家卫生城市”知识竞赛,为了了解本次竞赛成绩分布情况,竞赛组委会从中随机抽取部分学生的成绩(得分都是整数)作为样本,绘制成频率分布直方图如图,请根据提供的信息估计该区本次竞赛成绩在89.5分-99.5分的学生大约有900名. 如图,△ABC中,AB=AC,点D、E分别在AB、AC边上,∠EBC=∠DCB
如图,△ABC中,AB=AC,点D、E分别在AB、AC边上,∠EBC=∠DCB