题目内容

14．矩形周长为16cm，它的一边长为xcm，面积为ycm2，求y与x之间的函数关系式，当边长取多少时，面积最大？最大是多少？

分析 根据周长公式，可得另一条边的长，根据矩形的面积公式，可得函数解析式，根据二次函数的性质，可得函数的最大值．

解答 解：矩形另一条边的长为（8-x）xm，
矩形面积为S=x（8-x）=-x2+8x，
配方，得
S=-（x-4）2+16，
当x=4时，S最大=16．

点评 本题考查了二次函数的最值，利用矩形的面积公式得出函数解析式是解题关键．

练习册系列答案
相关题目
4．解方程：．
（1）x2-2x=0
（2）（x-1）2=4
（3）x2+2x-35=0
（4）x2-2x+1=0
（5）x（x-1）-2（x-1）=0
（6）（x-2）（x-1）=6．
5．已知y=$\sqrt{x-3}$-$\sqrt{3-x}$-1，求x+y=2．
2．使得等式$\frac{\sqrt{{x}^{2}-1}}{\sqrt{x-1}}$=$\sqrt{\frac{{x}^{2}-1}{x-1}}$=$\sqrt{x+1}$成立的x的取值范围是x≥-1．
9．二次函数y=a（x-h）2+k的图象是一条抛物线，其对称轴是直线x=h，顶点坐标是（h，k），它的图象与y=ax2的图象形状相同，只是位置不同，它的图象可由抛物线y=ax2经过左或右，上或下平移而得到．
19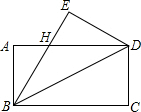．如图，将一块长方形的纸片ABCD沿BD翻折后，点C与E重合，若∠ADB=30°，EH=4cm，则BC的长度为（　　）
A．10cmB．12cmC．13cmD．14cm
6．一元二次方程x2-3x-1=0和x2+4x+6=0的所有实数根的和为（　　）
A．3B．-4C．-1D．7
3．下列各数中0、21、-$\frac{2}{5}$、-25%、$\frac{π}{3}$、-|-2-3|、0.$\stackrel{••}{63}$、3.14-π、-$\frac{22}{7}$，整数的个数为x，非负数的个数是y，分数的个数是z，则x+y+z的值为11．
4．已知x，y为实数，且y=$\frac{\sqrt{{x}^{2}-4}+\sqrt{4{-x}^{2}}+1}{2}$，则x+y=$\frac{5}{2}$或-$\frac{3}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网