题目内容
9.二次函数y=a(x-h)2+k的图象是一条抛物线,其对称轴是直线x=h,顶点坐标是(h,k),它的图象与y=ax2的图象形状相同,只是位置不同,它的图象可由抛物线y=ax2经过左或右,上或下平移而得到.分析 根据二次函数图象与几何变换和二次函数的性质求解.
解答 解:二次函数y=a(x-h)2+k的图象是一条抛物线,其对称轴是直线 x=h,顶点坐标是 (h,k),它的图象与y=ax2的图象形状相同,只是位置不同,它的图象可由抛物线 y=ax2经过左或右,上或下平移而得到.
故答案是:x=h;(h,k);y=ax2.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.也考查了二次函数的性质.

练习册系列答案
相关题目
19.已知反比例函数y=$\frac{k}{x}$的图象位于第一、第三象限,则k的取值范围是( )
| A. | k≥0 | B. | k>0 | C. | k≤0 | D. | k<0 |
18.某检修小组乘车从A地出发,在东西方向的马路上检修线路,如规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下(单位:km):
(1)求收工时检修小组距A地多远?
(2)当检修小组返回A地时,若该汽车每千米耗油0.2升,问共耗油多少升?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -4 | +7 | -9 | +8 | +6 | -5 | -2 |
(2)当检修小组返回A地时,若该汽车每千米耗油0.2升,问共耗油多少升?
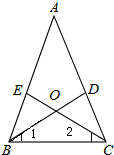 如图.在△ABC中,AB=AC,∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACB,BD与CE交于点O,∠BOC的大小与∠A的大小有什么关系?若∠1=$\frac{1}{3}$∠ABC,∠2=$\frac{1}{3}$∠ACB,则∠BOC与∠A的大小有什么关系?若∠1=$\frac{1}{n}$∠ABC,∠2=$\frac{1}{n}$∠ACB,则∠BOC与∠A的大小有什么关系?
如图.在△ABC中,AB=AC,∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACB,BD与CE交于点O,∠BOC的大小与∠A的大小有什么关系?若∠1=$\frac{1}{3}$∠ABC,∠2=$\frac{1}{3}$∠ACB,则∠BOC与∠A的大小有什么关系?若∠1=$\frac{1}{n}$∠ABC,∠2=$\frac{1}{n}$∠ACB,则∠BOC与∠A的大小有什么关系?