题目内容
18. 如图,当刻度尺的一边与⊙O相切时,另一边与⊙O的两个交点处的读数如图所示(单位:cm),圆的半径是5,那么刻度尺的宽度为( )
如图,当刻度尺的一边与⊙O相切时,另一边与⊙O的两个交点处的读数如图所示(单位:cm),圆的半径是5,那么刻度尺的宽度为( )| A. | $\frac{25}{6}$cm | B. | 4cm | C. | 3cm | D. | 2cm |
分析 连接OA,过点O作OD⊥AB于点D,由垂径定理可知,AD=$\frac{1}{2}$AB=$\frac{1}{2}$(9-1)=4,由OA=5,则OD=5-DE,在Rt△OAD中利用勾股定理求出r的值即可.
解答  解:连接OA,过点O作OD⊥AB于点D,
解:连接OA,过点O作OD⊥AB于点D,
∵OD⊥AB,
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$(9-1)=4cm,
∵OA=5,则OD=5-DE,
在Rt△OAD中,
OA2-OD2=AD2,即52-(5-DE)2=42,
解得DE=2cm.
故选D.
点评 本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
13.把方程x2-6x+4=0的左边配成完全平方,正确的变形是( )
| A. | (x-3)2=9 | B. | (x-3)2=13 | C. | (x+3)2=5 | D. | (x-3)2=5 |
3.若分式$\frac{{x}^{2}-9}{x-3}$的值为0,则x的值等于( )
| A. | 0 | B. | ±3 | C. | 3 | D. | -3 |
 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.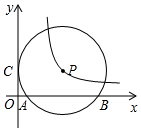 如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(9,0).双曲线y=$\frac{k}{x}$恰好经过圆心P,那么k的值是15.
如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(9,0).双曲线y=$\frac{k}{x}$恰好经过圆心P,那么k的值是15.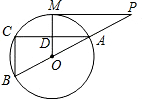 如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,交OM于点D.
如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,交OM于点D. 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2).
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2).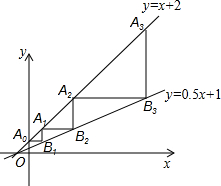 如图,直线y=x+2与y轴相交于点A0,过点A0作x轴的平行线交直线y=0.5x+1于点B1,过点B1作y轴的平行线交直线y=x+2于点A1,再过点A1作x轴的平行线交直线y=0.5x+1于点B2,过点B2作y轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x+1上的点B1,B2,B3,…,则An-1Bn的长为2n.
如图,直线y=x+2与y轴相交于点A0,过点A0作x轴的平行线交直线y=0.5x+1于点B1,过点B1作y轴的平行线交直线y=x+2于点A1,再过点A1作x轴的平行线交直线y=0.5x+1于点B2,过点B2作y轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x+1上的点B1,B2,B3,…,则An-1Bn的长为2n. 一个正方体,六个面分别写着六个连续的整数,且每个相对面上的两个数之和相等,如图所示,你能看到的数为7,10,11,则六个整数的和为( )
一个正方体,六个面分别写着六个连续的整数,且每个相对面上的两个数之和相等,如图所示,你能看到的数为7,10,11,则六个整数的和为( )