题目内容
6.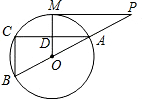 如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,交OM于点D.
如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,交OM于点D.(1)求证:MO∥BC;
(2)若DM=2,AC=6,求⊙O的半径.
分析 (1)由切线的性质可知OM⊥MP,结合条件可证得MO⊥AC,由圆周角定理可求得∠BCA=90°,则可证得BC∥OM;
(2)连接OC,设半径为r,则可知OC=OM=r,由垂径定理可求得CD,在Rt△COD中,利用勾股定理可列方程,可求得圆的半径.
解答 (1)证明:
∵MP切⊙O于点M,
∴OM⊥MP,
∵AC∥MP,
∴OM⊥AC,
∴∠ODA=90°,
∵AB是直径,
∴∠BCA=90°,
∴MO∥BC;
(2)解:
连结OC,设⊙O的半径为r,则OC=OM=r.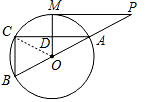
∵OM⊥AC,
∴CD=$\frac{1}{2}$AC=3,OD=OM-DM=r-2,
在Rt△OCD中,OC2=OD2+CD2,即r2=(r-2)2+32,
解得,r=$\frac{13}{4}$,即⊙O的半径为$\frac{13}{4}$.
点评 本题主要考查切线的性质,掌握过切点的半径与切线垂直是解题的关键.

练习册系列答案
相关题目
18. 如图,当刻度尺的一边与⊙O相切时,另一边与⊙O的两个交点处的读数如图所示(单位:cm),圆的半径是5,那么刻度尺的宽度为( )
如图,当刻度尺的一边与⊙O相切时,另一边与⊙O的两个交点处的读数如图所示(单位:cm),圆的半径是5,那么刻度尺的宽度为( )
 如图,当刻度尺的一边与⊙O相切时,另一边与⊙O的两个交点处的读数如图所示(单位:cm),圆的半径是5,那么刻度尺的宽度为( )
如图,当刻度尺的一边与⊙O相切时,另一边与⊙O的两个交点处的读数如图所示(单位:cm),圆的半径是5,那么刻度尺的宽度为( )| A. | $\frac{25}{6}$cm | B. | 4cm | C. | 3cm | D. | 2cm |
15.观察下面的一列二次根式,并填空:
(1)第n个二次根式可表示为$\sqrt{{n}^{2}+n}$.(用含n的代数式表示).
(2)通过观察估算:第16个二次根式的值在16和17这两个连续正数之间.
| 第1个 | 第2个 | 第3个 | 第4个 | … |
| $\sqrt{{1^2}+1}$ | $\sqrt{{2^2}+2}$ | $\sqrt{{3^2}+3}$ | $\sqrt{{4^2}+4}$ | … |
(2)通过观察估算:第16个二次根式的值在16和17这两个连续正数之间.
16. 一个表面标有汉字的多面体的平面展开图如图所示,如果“你”在上面,“乐”在前面,则不正确的是( )
一个表面标有汉字的多面体的平面展开图如图所示,如果“你”在上面,“乐”在前面,则不正确的是( )
 一个表面标有汉字的多面体的平面展开图如图所示,如果“你”在上面,“乐”在前面,则不正确的是( )
一个表面标有汉字的多面体的平面展开图如图所示,如果“你”在上面,“乐”在前面,则不正确的是( )| A. | “年”在下面 | B. | “祝”在后面 | C. | “新”在左边 | D. | “快”在左边 |
 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则R与r之间的关系是R=4r.
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则R与r之间的关系是R=4r.
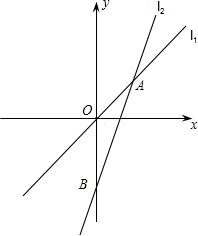 如图,在平面直角坐标系中,直线l1:y=$\frac{4}{3}$x与直线l2:y=kx+b相交于点A,点A的横坐标为3,直线l2交y轴于点B,且OA=$\frac{1}{2}$OB.
如图,在平面直角坐标系中,直线l1:y=$\frac{4}{3}$x与直线l2:y=kx+b相交于点A,点A的横坐标为3,直线l2交y轴于点B,且OA=$\frac{1}{2}$OB. 对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).