题目内容
5.已知在平行四边形ABCD中,点M、N分别是边BC、CD的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么向量$\overrightarrow{MN}$关于$\overrightarrow{a}$、$\overrightarrow{b}$的分解式是( )| A. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ |
分析 首先根据题意画出图形,然后连接BD,由三角形法则,求得$\overrightarrow{BD}$,又由点M、N分别是边BC、CD的中点,根据三角形中位线的性质,即可求得答案.
解答 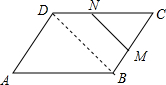 解:如图,连接BD,
解:如图,连接BD,
∵在平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,
∴$\overrightarrow{BD}$=$\overrightarrow{AD}$-$\overrightarrow{AB}$=$\overrightarrow{b}$-$\overrightarrow{a}$,
∵点M、N分别是边BC、CD的中点,
∴MN∥BD,MN=$\frac{1}{2}$BD,
∴$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{BD}$=$\frac{1}{2}$($\overrightarrow{b}$-$\overrightarrow{a}$)=-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$.
故选B.
点评 此题考查了平面向量的知识以及三角形的中位线的性质.注意结合题意画出图形,利用图形求解是关键.

练习册系列答案
相关题目
6.在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则树的高度为( )
| A. | 10米 | B. | 9.6米 | C. | 6.4米 | D. | 4.8米 |
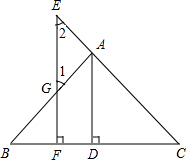 已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC.
已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC.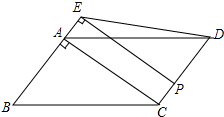 如图,在?ABCD中,AB=3,BC=5,对角线AC⊥AB,点P从点D出发,沿折线DC-CB以每秒1个单位长度的速度项终点B运动(不与点B、D重合),过点P作PE⊥AB,交射线BA于点E,连接PD、DE.设点P的运动时间为t(秒),△PDE与?ABCD重叠部分图形的面积为S(平方单位).
如图,在?ABCD中,AB=3,BC=5,对角线AC⊥AB,点P从点D出发,沿折线DC-CB以每秒1个单位长度的速度项终点B运动(不与点B、D重合),过点P作PE⊥AB,交射线BA于点E,连接PD、DE.设点P的运动时间为t(秒),△PDE与?ABCD重叠部分图形的面积为S(平方单位). 如图所示,已知AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=35°28′,则∠EGF=72°16′.
如图所示,已知AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=35°28′,则∠EGF=72°16′.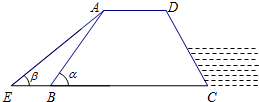 如图,防洪大堤的横断面是梯形ABCD,其中AD∥BC,坡角α=60°,汛期来临前对其进行了加固,改造后的坡长为AE,背水面坡角β=45°.若原坡长AB=16m,求改造后的坡长AE(结果保留根号).
如图,防洪大堤的横断面是梯形ABCD,其中AD∥BC,坡角α=60°,汛期来临前对其进行了加固,改造后的坡长为AE,背水面坡角β=45°.若原坡长AB=16m,求改造后的坡长AE(结果保留根号).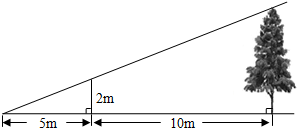 如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )
如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )