题目内容
20.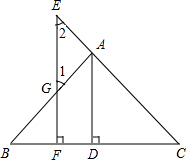 已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC.
已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC.填写分析和证明中的空白.
分析:要证明AD平分∠BAC,只要证明∠BAD=∠ADC而已知∠1=∠2,所以应联想这两个角分别和∠1、∠2得到关系,由已知BC的两条垂线可推出EF∥AD,这时再观察这两对角的关系已不难得到结论.
证明:
∵AD⊥BC,EF⊥BC(已知)
∴EF∥AD(同位角相等,两直线平行)
∴∠1=∠BAD(两直线平行,内错角相等)
∠2=∠CAD(两直线平行,同位角角相等)
∵∠1=∠2(已知)
∴∠BAD=∠ADC(等量代换)
∴AD平分∠BAC(角平分线的定义)
分析 根据垂直定义得出∠ADC=∠EFC,根据平行线的判定推出AD∥EF,根据平行线的性质推出∠1=∠BAD,∠2=∠CAD,推出∠BAD=∠CAD即可.
解答 证明:∵AD⊥BC,EF⊥BC,
∴∠ADC=∠EFC=90°,
∴AD∥EF(同位角相等,两直线平行),
∴∠1=∠BAD(两直线平行,内错角相等),
∠2=∠DAC(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠BAD=∠DAC(等量代换),
∴AD平分∠BAC,
故答案为:∠ADC;AD;AD,同位角相等,两直线平行;∠BAD;∠CAD;∠ADC.
点评 本题考查了平行线的性质和判定,解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
相关题目
5.已知在平行四边形ABCD中,点M、N分别是边BC、CD的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么向量$\overrightarrow{MN}$关于$\overrightarrow{a}$、$\overrightarrow{b}$的分解式是( )
| A. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ |
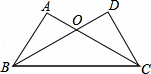 在△ABC和△DCB中,AC,BD交于点O,AB=DC,AC=BD.求证:(1)△ABC≌△DCB:(2)OB=OC.
在△ABC和△DCB中,AC,BD交于点O,AB=DC,AC=BD.求证:(1)△ABC≌△DCB:(2)OB=OC.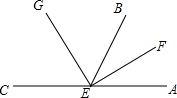 如图,EF、EG分别是∠AEB、∠BEC的平分线,求∠GEF的度数.
如图,EF、EG分别是∠AEB、∠BEC的平分线,求∠GEF的度数. 如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是-1.
如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是-1.
 某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部分计划将阴影部分进行绿化,中间修建一座雕像.
某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部分计划将阴影部分进行绿化,中间修建一座雕像.