题目内容
15．
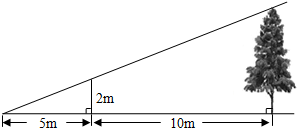如图，为了测量某棵树的高度，小明用长为2m的竹竿作测量工具，移动竹竿，使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点．此时竹竿与这一点相距5m，与树相距10m，则树的高度为（ ）| A． | 5m | B． | 6m | C． | 7m | D． | 8m |
分析 先判定△OAB和△OCD相似，再根据相似三角形对应边成比例列式求解即可．
解答 解：如图所示：
∵AB⊥OD，CD⊥OD，
∴AB∥CD，
∴△OAB∽△OCD，
∴$\frac{AB}{CD}=\frac{OB}{OD}$，
即$\frac{2}{CD}=\frac{5}{5+10}$，
解得：CD=6（米）；
即树的高度为6m；
故选：B．
点评 本题考查了相似三角形的应用，判断出三角形相似并根据相似三角形对应边成比例得出比例式是解题的关键．
练习册系列答案
相关题目
5．已知在平行四边形ABCD中，点M、N分别是边BC、CD的中点，如果$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，那么向量$\overrightarrow{MN}$关于$\overrightarrow{a}$、$\overrightarrow{b}$的分解式是（ ）
| A． | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B． | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C． | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D． | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ |
6．
在如图的地板行走，随意停下来时，站在黑色地板上的概率是（ ）
在如图的地板行走，随意停下来时，站在黑色地板上的概率是（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{1}{4}$ |
3．下列运算正确的是（ ）
| A． | （a+b）2=a2+b2 | B． | （-2a2b）3=-8a5b3 | C． | a6÷a3=a2 | D． | a3•a2=a5 |
10．
某市有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，规划部分计划将阴影部分进行绿化，中间修建一座雕像．
（1）请用含a，b的代数式表示绿化面积s；
（2）当a=3，b=2时，求绿化面积s．
某市有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，规划部分计划将阴影部分进行绿化，中间修建一座雕像．（1）请用含a，b的代数式表示绿化面积s；
（2）当a=3，b=2时，求绿化面积s．
如图，在Rt△ABC中，∠C=90°，D是AC边上一点，DE⊥AB于点E．若DE=2，BC=3，AC=6，求AE的长．
5．如图银行标志中，是轴对称图形的个数为（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |