Question

14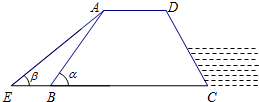．如图，防洪大堤的横断面是梯形ABCD，其中AD∥BC，坡角α=60°，汛期来临前对其进行了加固，改造后的坡长为AE，背水面坡角β=45°．若原坡长AB=16m，求改造后的坡长AE（结果保留根号）．

Answer 1

分析 过A作AH⊥BC于H，在Rt△ABH中求出AH的长度，然后在Rt△AEH中求出AE的长度．

解答 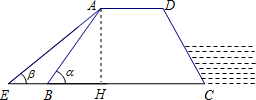解：过A作AH⊥BC于H．
在Rt△ABH中，
∵α=60°，AB=16m，
∴AH=AB•sinα=16×$\frac{\sqrt{3}}{2}$=8$\sqrt{3}$，
在Rt△AEH中，
∵β=45°，
∴AE=$\frac{AH}{sin45°}$=$\frac{8\sqrt{3}}{\frac{\sqrt{2}}{2}}$=8$\sqrt{6}$．
答：改造后的坡长AE为8$\sqrt{6}$m．

点评 本题考查了解直角三角形的应用，解答本题的关键是根据所给角构造直角三角形，利用三角函数的知识求解．