题目内容
13.利用一个圆及其若干条弦分别设计出符合下列条件的图案:(1)是轴对称图形但不是中心对称图形;
(2)是中心对称图形但不是轴对称图形;
(3)既是轴对称图形又是中心对称图形.
分析 (1)根据轴对称图形的特点设计图案即可;
(2)根据中心对称图形的特点设计图案即可;
(3)根据轴对称和中心对称图形的特点设计图案即可.
解答 解:(1)如图1所示:
(2)如图2所示:
(3)如图3所示:
点评 本题主要考查的是图案设计,掌握轴对称图形的性质和中心对称图形的性质是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
1.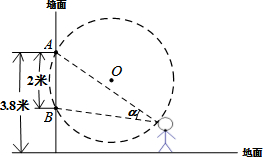 某学校为了提升学生素质,要求学生利用休息时间参加社会实践活动.四月的一个星期天,该校学生小慧去市美术馆参观“中国梦•精品中国画”美术作品展.据展览说明介绍,参观作品时人眼看作品的视角α是30°时欣赏美术作品的效果最佳.当小慧看到一幅2米×2米的作品时(如图所示)发现该作品挂在墙面上的顶端A点距离地面3.8米.若小慧的眼睛距离地面1.60米,当看到该作品的效果达到最佳时,小慧的眼睛距离挂美术作品的墙面的最远距离是( )
某学校为了提升学生素质,要求学生利用休息时间参加社会实践活动.四月的一个星期天,该校学生小慧去市美术馆参观“中国梦•精品中国画”美术作品展.据展览说明介绍,参观作品时人眼看作品的视角α是30°时欣赏美术作品的效果最佳.当小慧看到一幅2米×2米的作品时(如图所示)发现该作品挂在墙面上的顶端A点距离地面3.8米.若小慧的眼睛距离地面1.60米,当看到该作品的效果达到最佳时,小慧的眼睛距离挂美术作品的墙面的最远距离是( )
 某学校为了提升学生素质,要求学生利用休息时间参加社会实践活动.四月的一个星期天,该校学生小慧去市美术馆参观“中国梦•精品中国画”美术作品展.据展览说明介绍,参观作品时人眼看作品的视角α是30°时欣赏美术作品的效果最佳.当小慧看到一幅2米×2米的作品时(如图所示)发现该作品挂在墙面上的顶端A点距离地面3.8米.若小慧的眼睛距离地面1.60米,当看到该作品的效果达到最佳时,小慧的眼睛距离挂美术作品的墙面的最远距离是( )
某学校为了提升学生素质,要求学生利用休息时间参加社会实践活动.四月的一个星期天,该校学生小慧去市美术馆参观“中国梦•精品中国画”美术作品展.据展览说明介绍,参观作品时人眼看作品的视角α是30°时欣赏美术作品的效果最佳.当小慧看到一幅2米×2米的作品时(如图所示)发现该作品挂在墙面上的顶端A点距离地面3.8米.若小慧的眼睛距离地面1.60米,当看到该作品的效果达到最佳时,小慧的眼睛距离挂美术作品的墙面的最远距离是( )| A. | 4米 | B. | 2$\sqrt{3}$米 | C. | (2+$\sqrt{3}$)米 | D. | ($\sqrt{3}$+1.6)米 |
5.已知在平行四边形ABCD中,点M、N分别是边BC、CD的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么向量$\overrightarrow{MN}$关于$\overrightarrow{a}$、$\overrightarrow{b}$的分解式是( )
| A. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ |
3.下列运算正确的是( )
| A. | (a+b)2=a2+b2 | B. | (-2a2b)3=-8a5b3 | C. | a6÷a3=a2 | D. | a3•a2=a5 |
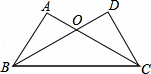 在△ABC和△DCB中,AC,BD交于点O,AB=DC,AC=BD.求证:(1)△ABC≌△DCB:(2)OB=OC.
在△ABC和△DCB中,AC,BD交于点O,AB=DC,AC=BD.求证:(1)△ABC≌△DCB:(2)OB=OC.