题目内容
计算
×
= .
| 20082+2006 |
| 20062-2008 |
| 40102-8020 |
| 2006×2009-4 |
考点:有理数无理数的概念与运算
专题:应用题
分析:将20082变成(2006+2)2,将20062变成(2008-2)2,从而可将前半部分分解成因式相乘的形式,然后将40102-8020写成40102-8020-1+1的形式,将2006×2009-4写成(2008-2)(2008+1)-4的形式,从而可将后半部分分解成因式相乘的形式,综合两部分,约分后可得出答案.
解答:解:原式=
×
=
×
=
×
=
×
=
=4.
故答案为:4.
| (2006+2)2+2006 |
| (2008-2)2-2008 |
| 40102-2×4010+1-1 |
| (2008-2)(2008+1)-4 |
=
| 20062+5×2006+4 |
| 20082-5×2008+4 |
| (4010-1)2-1 |
| 20082-2008-6 |
=
| (2006+1)(2006+4) |
| (2008-1)(2008-4) |
| 4010×4008 |
| (2008-3)(2008+2) |
=
| 2010 |
| 2004 |
| 4×2005×2004 |
| 2005×2010 |
=
| 4×2005 |
| 2005 |
=4.
故答案为:4.
点评:此题考查了有理数无理数的运算,解答本题的关键是将分子分母进行拆分,达到分解成因式相乘的形式,难度较大.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
设a=
-
,那么a是( )
| 3 | 12
| ||||||
| 3 | 7 |
| A、无理数 | B、正整数 |
| C、分数 | D、负整数 |
若正六边形的外接圆的半径为R,则这个正六边形的面积为( )
A、
| ||||
| B、6R2 | ||||
C、
| ||||
| D、6R |
若一个凸多边形的边数恰好是从某个顶点引出的对角线的条数的
倍,则这个多边形的内角和是( )
| 4 |
| 3 |
| A、1080° |
| B、1540° |
| C、1800° |
| D、2160° |
圆的直径是13cm,如果直线与圆心的距离为4.5cm,那么直线与圆公共点有( )
| A、1个 | B、2个 | C、3个 | D、0个 |
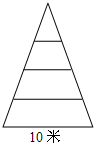 如图,是一轴截面为等腰三角形的古塔,塔基圆直径为10米,塔共四层,每层高3米,天意广告公司欲沿塔面悬挂一幅公益广告条幅,要求条幅不能铺在地面上,也不能高于塔顶,则条幅的最大长度为
如图,是一轴截面为等腰三角形的古塔,塔基圆直径为10米,塔共四层,每层高3米,天意广告公司欲沿塔面悬挂一幅公益广告条幅,要求条幅不能铺在地面上,也不能高于塔顶,则条幅的最大长度为