题目内容
5.在平面直角坐标系xOy中,抛物线y=-x2+3x+4与直线y=-x+$\frac{9}{2}$围成一个封闭区域(包含边界).现有A、B两个装有除标号外完全相同的若干小球的不透明布袋,A布袋内小球分别标有数字0,1,2,3,B布袋内小球上分别标有数字4,5,6,分别从A、B两个布袋中随机取出一个小球,分别将其号码作为袋内P的横坐标及纵坐标,则点P落在封闭区域内的概率为$\frac{7}{12}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与点P落在封闭区域内的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有12种等可能的结果,点P落在封闭区域内的有:(1,4),(1,5),(1,6),(2,4)(2,5),(2,6),(3,4),
∴点P落在封闭区域内的概率为:$\frac{7}{12}$.
故答案为:$\frac{7}{12}$.
点评 此题考查了列表法或树状图法求概率以及一次函数与二次函数的交点问题.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
10.某城市自来水收费实行阶梯水价,收费标准如表所示,某用户5月份交水费42元,则所用水为19方.
| 月用水量 | 不超过12方的部分 | 超过12方不超过18方的部分 | 超过18方的部分 |
| 收费标准(元/方) | 2 | 2.5 | 3 |
14.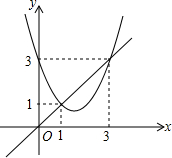 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2-4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b-1)x+c<0;⑤(1+c)2<b2
正确结论的个数是( )
 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2-4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b-1)x+c<0;⑤(1+c)2<b2
正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.下列各组数据是三角形三条边的长,组成的三角形不是直角三角形的是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | 2,3,4 | D. | 5,12,13 |