题目内容
14.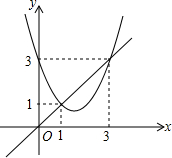 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2-4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b-1)x+c<0;⑤(1+c)2<b2
正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①由函数y=x2+bx+c与x轴无交点,可得b2-4c<0;
②当x=1时,y=1+b+c=1;
③当x=3时,y=9+3b+c=3;
④当1<x<3时,二次函数值小于一次函数值,可得x2+bx+c<x,继而可求得答案;
⑤根据对称轴方程得到b的值;由抛物线与y轴的交点坐标得到c的值,代入数值进比较即可.
解答 解:①∵函数y=x2+bx+c与x轴无交点,
∴b2-4ac<0;
故①错误;
②当x=1时,y=1+b+c=1,
故②错误;
③∵当x=3时,y=9+3b+c=3,
∴3b+c+6=0;
故③正确;
④∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b-1)x+c<0.
故④正确.
⑤如图所示,抛物线与y轴的交点坐标是(0,3),则c=3.
对称轴x=-$\frac{b}{2}$=$\frac{0+3}{2}$,则b=-3,
所以(1+c)2=(1+3)2=16,b2=(-3)2=9,
则(1+c)2>b2,
故⑤错误.
综上所述,正确的结论有2个.
故选:B.
点评 主要考查图象与二次函数系数之间的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
相关题目
 已知一次函数的图象经过点A(2,3),B(0,-2).
已知一次函数的图象经过点A(2,3),B(0,-2).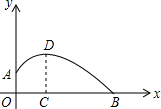 如图,一个运动员推铅球,铅球在点A处出手,出手时铅球离地面约1.6m,铅球落地点在点B处,铅球运行中在运动员前4m(即OC=4)达到最高点,最高点距离地面高度为3.2m,已知铅球经过的路线是抛物线,试在图示的直面坐标系中计算这个运动员的成绩.
如图,一个运动员推铅球,铅球在点A处出手,出手时铅球离地面约1.6m,铅球落地点在点B处,铅球运行中在运动员前4m(即OC=4)达到最高点,最高点距离地面高度为3.2m,已知铅球经过的路线是抛物线,试在图示的直面坐标系中计算这个运动员的成绩.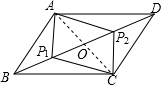 如图所示,在平行四边形ABCD中,BP1=DP2,求证:四边形AP1CP2是平行四边形.
如图所示,在平行四边形ABCD中,BP1=DP2,求证:四边形AP1CP2是平行四边形.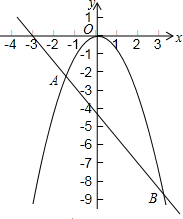 如图所示,抛物线${y_1}=-{x^2}$与直线${y_2}=-\frac{3}{2}x-\frac{9}{2}$交于A,B两点.
如图所示,抛物线${y_1}=-{x^2}$与直线${y_2}=-\frac{3}{2}x-\frac{9}{2}$交于A,B两点.