题目内容
16.利用图解二元一次方程组.$\left\{\begin{array}{l}{x+y=3}\\{3x-y=5}\end{array}\right.$.分析 先画出直线x+y=3、直线3x-y=5,再找出它们的交点坐标,然后根据函数图象交点坐标为两函数解析式组成的方程组的解即可得到方程组$\left\{\begin{array}{l}{x+y=3}\\{3x-y=5}\end{array}\right.$的解.
解答 解:如图,直线x+y=3和直线3x-y=5的交点坐标为(2,1),
所以方程组$\left\{\begin{array}{l}{x+y=3}\\{3x-y=5}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.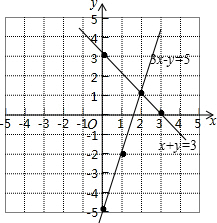
点评 本题主要考查了一次函数与二元一次方程(组):满足解析式的点就在函数的图象上,在函数的图象上的点,就一定满足函数解析式.函数图象交点坐标为两函数解析式组成的方程组的解.也考查了一次函数图象.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
8.设a=$\sqrt{{4}^{2}}$,则a3-a2=( )
| A. | 2 | B. | 48 | C. | 6 | D. | 8 |
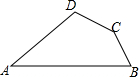 如图,在四边形ABCD中,∠A=30°,∠B=60°,AB=8,BC=2,AD=3$\sqrt{3}$.求四边形ABCD的面积.
如图,在四边形ABCD中,∠A=30°,∠B=60°,AB=8,BC=2,AD=3$\sqrt{3}$.求四边形ABCD的面积.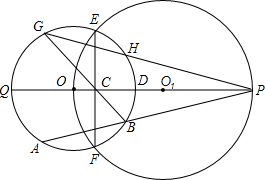 如图,⊙O1经过⊙O的圆心,E、F是两圆的交点,直线OO1交⊙O于点Q、D,交⊙O1于点P,交EF于点C,点A在劣弧QF上运动(与点Q、F不重合),连结PA交弧DF于B,连结BC并延长交⊙O于点G,连结PG交⊙O于点H.求证:
如图,⊙O1经过⊙O的圆心,E、F是两圆的交点,直线OO1交⊙O于点Q、D,交⊙O1于点P,交EF于点C,点A在劣弧QF上运动(与点Q、F不重合),连结PA交弧DF于B,连结BC并延长交⊙O于点G,连结PG交⊙O于点H.求证: 已知一次函数的图象经过点A(2,3),B(0,-2).
已知一次函数的图象经过点A(2,3),B(0,-2).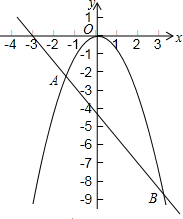 如图所示,抛物线${y_1}=-{x^2}$与直线${y_2}=-\frac{3}{2}x-\frac{9}{2}$交于A,B两点.
如图所示,抛物线${y_1}=-{x^2}$与直线${y_2}=-\frac{3}{2}x-\frac{9}{2}$交于A,B两点.