题目内容
9.解不等式(组).(1)4x-3>2x+5(把解集在数轴上表示出来)
(2)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1-3(x-1)<8-x}\end{array}\right.$.
分析 (1)根据不等式的性质解答即可;
(2)先解不等式组中的每一个不等式,得到不等式组的解集,再把不等式的解集表示在数轴上即可.
解答 解:(1)移项,得4x-2x>5+3,
合并同类项,得2x>8,
系数化为1,得x>4.
在数轴上表示为 ;
;
(2)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1①}\\{1-3(x-1)<8-x②}\end{array}\right.$
解不等式①得,x≤1;
解不等式②得,x>-2,
所以原不等式组的解集为:-2<x≤1.
点评 本题主要考查了解一元一次不等式及不等式组,关键是掌握不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
8.下列运算正确的是( )
| A. | a2•a2=2a2 | B. | a2+a2=a4 | C. | (1+2a)2=1+2a+4a2 | D. | (-a+1)(a+1)=1-a2 |
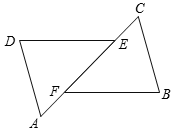 如图,△ADE与△CBF的边AE、CF在同一条直线上,DE∥BF,AD∥BC,AF=CE,求证:△ADE≌△CBF.
如图,△ADE与△CBF的边AE、CF在同一条直线上,DE∥BF,AD∥BC,AF=CE,求证:△ADE≌△CBF.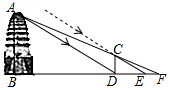 如图是位于陕西省西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.小铭、小希等几位同学想利用一些测量工具和所学的几何知识测量小雁塔的高度,由于观测点与小雁塔底部间的距离不易测量,因此经过研究需要进行两次测量,于是在阳光下,他们首先利用影长进行测量,方法如下:小铭在小雁塔的影子顶端D处竖直立一根木棒CD,并测得此时木棒的影长DE=2.4米;然后,小希在BD的延长线上找出一点F,使得A、C、F三点在同一直线上,并测得DF=2.5米.已知图中所有点均在同一平面内,木棒高CD=1.72米,AB⊥BF,CD⊥BF,试根据以上测量数据,求小雁塔的高度AB.
如图是位于陕西省西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.小铭、小希等几位同学想利用一些测量工具和所学的几何知识测量小雁塔的高度,由于观测点与小雁塔底部间的距离不易测量,因此经过研究需要进行两次测量,于是在阳光下,他们首先利用影长进行测量,方法如下:小铭在小雁塔的影子顶端D处竖直立一根木棒CD,并测得此时木棒的影长DE=2.4米;然后,小希在BD的延长线上找出一点F,使得A、C、F三点在同一直线上,并测得DF=2.5米.已知图中所有点均在同一平面内,木棒高CD=1.72米,AB⊥BF,CD⊥BF,试根据以上测量数据,求小雁塔的高度AB.