题目内容
20.计算:(1)2$\sqrt{3}$-3$\sqrt{5}$-$\sqrt{5}$+5$\sqrt{5}$+7$\sqrt{3}$
(2)$\sqrt{12}$-$\sqrt{27}$-$\sqrt{20}$+$\sqrt{50}$
(3)$\sqrt{4x}$+2$\sqrt{2x}$-$\frac{1}{2}\sqrt{8x}$-4$\sqrt{x}$(x≥0)
(4)$\sqrt{\frac{1}{2}}$-$\sqrt{8}$+$\frac{1}{\sqrt{2}}$-$\frac{1}{\sqrt{8}}$.
分析 (1)直接将同类二次根式进行加减运算即可;
(2)首先化简二次根式,进而合并同类二次根式进行加减运算即可;
(3)首先化简二次根式,进而合并同类二次根式进行加减运算即可;
(4)首先化简二次根式,进而合并同类二次根式进行加减运算即可.
解答 解:(1)2$\sqrt{3}$-3$\sqrt{5}$-$\sqrt{5}$+5$\sqrt{5}$+7$\sqrt{3}$
=(2$\sqrt{3}$+7$\sqrt{3}$)+(-3$\sqrt{5}$-$\sqrt{5}$+5$\sqrt{5}$)
=9$\sqrt{3}$+$\sqrt{5}$;
(2)$\sqrt{12}$-$\sqrt{27}$-$\sqrt{20}$+$\sqrt{50}$
=2$\sqrt{3}$-3$\sqrt{3}$-2$\sqrt{5}$+5$\sqrt{2}$
=-$\sqrt{3}$-2$\sqrt{5}$+5$\sqrt{2}$;
(3)$\sqrt{4x}$+2$\sqrt{2x}$-$\frac{1}{2}\sqrt{8x}$-4$\sqrt{x}$(x≥0)
=2$\sqrt{x}$+2$\sqrt{2x}$-$\sqrt{2x}$-4$\sqrt{x}$
=-2$\sqrt{x}$+$\sqrt{2x}$;
(4)$\sqrt{\frac{1}{2}}$-$\sqrt{8}$+$\frac{1}{\sqrt{2}}$-$\frac{1}{\sqrt{8}}$
=$\frac{\sqrt{2}}{2}$-2$\sqrt{2}$+$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{4}$
=-$\frac{5\sqrt{2}}{4}$.
点评 此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案 如图,AB是⊙O直径,点C为⊙O上一点,∠C=20°,则∠BOC度数为( )
如图,AB是⊙O直径,点C为⊙O上一点,∠C=20°,则∠BOC度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 60° |
| A. | a6 | B. | -a6 | C. | -a5 | D. | a5 |
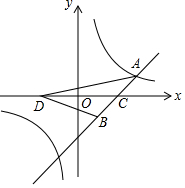 如图,一次函数y=ax-2(a≠0)的图象与反比例函数$y=\frac{k}{x}$(k≠0)的图象交于点A(m,1),且与x轴交于点C.点B(1,-1)在直线AC上.
如图,一次函数y=ax-2(a≠0)的图象与反比例函数$y=\frac{k}{x}$(k≠0)的图象交于点A(m,1),且与x轴交于点C.点B(1,-1)在直线AC上.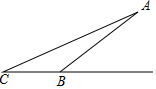 为了游客的安全,某景点将原坡角为30°的斜坡AB改为坡度为1:3的斜坡AC,已知AB=100米,BC在同一水平线上,求改造后斜坡的坡脚向前移动距离BC的长.
为了游客的安全,某景点将原坡角为30°的斜坡AB改为坡度为1:3的斜坡AC,已知AB=100米,BC在同一水平线上,求改造后斜坡的坡脚向前移动距离BC的长.