题目内容
18.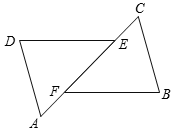 如图,△ADE与△CBF的边AE、CF在同一条直线上,DE∥BF,AD∥BC,AF=CE,求证:△ADE≌△CBF.
如图,△ADE与△CBF的边AE、CF在同一条直线上,DE∥BF,AD∥BC,AF=CE,求证:△ADE≌△CBF.
分析 根据平行线的性质,可得∠DEA=∠BFC,∠A=∠C;根据等式的性质,可得AE=CF,根据全等三角形的判定,可得答案.
解答 证明:∵DE∥BF,AD∥BC,
∴∠DEA=∠BFC,∠A=∠C.
∵AF=CE,
∴AF+FE=FE+CE
即AE=CF
在△ADE和△CBF中,$\left\{\begin{array}{l}{∠DEA=∠BFC}\\{AE=CF}\\{∠A=∠C}\end{array}\right.$,
∴△ADE≌△CBF(ASA).
点评 本题考查了全等三角形的判定,利用平行线的性质,等式的性质得出全等三角形的条件是解题关键.

练习册系列答案
相关题目
13. 将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )
将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )
 将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )
将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )| A. | $\frac{11π}{3}+2\sqrt{3}$ | B. | $3π+2\sqrt{3}$ | C. | $3π+\sqrt{3}$ | D. | $\frac{11π}{3}+\sqrt{3}$ |
7.如图是一个几何体的三视图,则这个几何体的表面积是( )
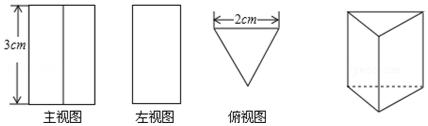

| A. | 18cm2 | B. | 20cm2 | C. | (18+2$\sqrt{3}$)cm2 | D. | (18+4$\sqrt{3}$)cm2 |
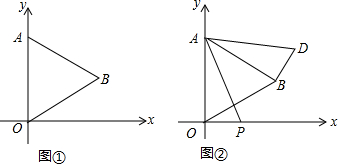
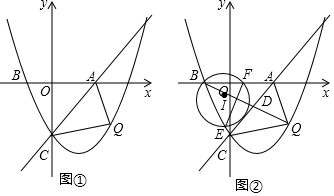
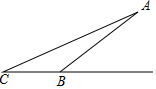 为了游客的安全,某景点将原坡角为30°的斜坡AB改为坡度为1:3的斜坡AC,已知AB=100米,BC在同一水平线上,求改造后斜坡的坡脚向前移动距离BC的长.
为了游客的安全,某景点将原坡角为30°的斜坡AB改为坡度为1:3的斜坡AC,已知AB=100米,BC在同一水平线上,求改造后斜坡的坡脚向前移动距离BC的长.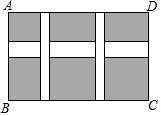 如图,某小区规划在一个长40米,宽36米的矩形场地ABCD上修建横、纵道路宽为3:2的三条道路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为198平方米,求道路的宽度.
如图,某小区规划在一个长40米,宽36米的矩形场地ABCD上修建横、纵道路宽为3:2的三条道路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为198平方米,求道路的宽度.