题目内容
13.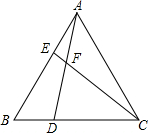 如图,在△ABC中,∠BAC=∠B=60°,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F,当点D、E在边BC、AB上运动时,∠DFC的度数是否发生变化?若不变,求出其度数;若变化,写出其变化规律.
如图,在△ABC中,∠BAC=∠B=60°,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F,当点D、E在边BC、AB上运动时,∠DFC的度数是否发生变化?若不变,求出其度数;若变化,写出其变化规律.
分析 只要证明△ABD≌△CAE,推出∠ACE=∠BAD,由∠CAF+∠BAD=60°,根据∠AFE=∠ACE+∠CAF=∠BAD+∠CAF=60°,由此即可证明.
解答 解:不变,
∵∠BAC=∠B=60°,
∴△ABC是等边三角形,
∴AB=AC,
在△ABD与△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠B=∠BAC}\\{BD=AE}\end{array}\right.$,
∴△ABD≌△CAE,
∴∠ACE=∠BAD,
∵∠CAF+∠BAD=60°,
∴AFE=∠ACE+∠CAF=∠BAD+∠CAF=60°.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质等知识,解题的关键是正确寻找全等三角形,理由全等三角形的性质解决问题,属于中考常考题型.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
3.下列事件中,属于随机事件的有( )
①太阳东升西落
②投一枚骰子得到的点数是奇数
③买一张彩票中一等奖
④从日历本上任选一天为星期天.
①太阳东升西落
②投一枚骰子得到的点数是奇数
③买一张彩票中一等奖
④从日历本上任选一天为星期天.
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
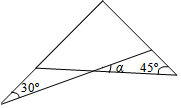 一副三角板如图所示叠放在一起,则∠α的度数是15°.
一副三角板如图所示叠放在一起,则∠α的度数是15°.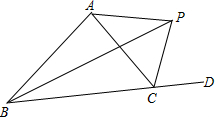 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,∠BPC=40°.
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,∠BPC=40°.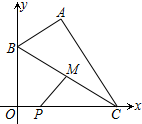 在平面直角坐标系中,已知A(2,4)、P(1,0),B为y轴上的动点,以AB为边构造△ABC,使点C在x轴上,∠BAC=90°.M为BC的中点,则PM的最小值为$\frac{4\sqrt{5}}{5}$.
在平面直角坐标系中,已知A(2,4)、P(1,0),B为y轴上的动点,以AB为边构造△ABC,使点C在x轴上,∠BAC=90°.M为BC的中点,则PM的最小值为$\frac{4\sqrt{5}}{5}$.