题目内容
1.6名乒乓球运动员穿着4种颜色的服装进行表演赛,其中2人穿红色的,2人穿黄色的,1人穿蓝色的,1人穿黑色的.每次表演选3人出场,且仅在服装颜色不同的选手间对局比赛,具体规则是:(1)出场的“3人组”中若服装均不相同,则每两人都进行1局比赛,且比赛过的2名选手在不同的“3人组”中再相遇时还要比赛.
(2)出场的“3人组”中若有服装相同的2名选手,则这2名选手之间不比赛,并且只派1人与另1名选手进行1局比赛.
按照这样的规则,当所有不同的“3人组”都出场后,共进行了44局比赛.
分析 将穿红色服装的2名选手表示为平行直线l1﹑l2;将穿黄色服装的2名选手表示为另两条平行直线l3﹑l4;将穿蓝色﹑黑色服装的选手表示为相交直线l5﹑l6﹑且与l1﹑l2﹑l3﹑l4均相交,这就得到了图1,图中无三线共点.(1)“3人组”的服装均不相同时,按规则,对应着3条直线两两相交,其比赛局数恰为图中的线段数(图2)因为l1﹑l2﹑l3﹑l4上各有4个交点,每条直线有6条线段,可求线段条数;(2)当“3人组”有2人服装相同,按规则,其比赛局数恰好为图中的线段数(图3)因为l5﹑l6上各有5个交点,每条直线上都有10条线段,可求线段条数;再相加即可求解.
解答 解:将穿红色服装的2名选手表示为平行直线l1﹑l2;将穿黄色服装的2名选手表示为另两条平行直线l3﹑l4;将穿蓝色﹑黑色服装的选手表示为相交直线l5﹑l6﹑且与l1﹑l2﹑l3﹑l4均相交,这就得到了图1,图中无三线共点.
(1)“3人组”的服装均不相同时,按规则,对应着3条直线两两相交,其比赛局数恰为图中的线段数(图2)因为l1﹑l2﹑l3﹑l4上各有4个交点,每条直线有6条线段,共有24条线段.
(2)当“3人组”有2人服装相同,按规则,其比赛局数恰好为图中的线段数(图3)因为l5﹑l6上各有5个交点,每条直线上都有10条线段,共得20条线段.
两种情况合计,总比赛局数为44局.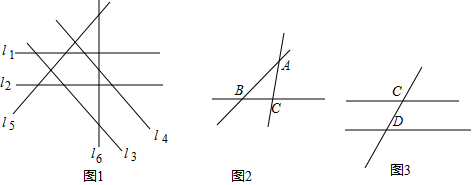
故答案为:44.
点评 此题考查了计数方法,解题的关键是分情况讨论及推理论证.注意数形思想的运用.

练习册系列答案
相关题目
17.下列奥运会徽中,轴对称图形是( )
| A. |  | B. |  | C. |  | D. |  |
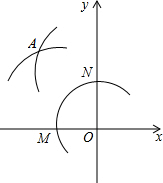 在平面直角坐标系中,在x轴的负半轴与y轴的正半轴上分别截取OM,ON,使OM=ON;再分别以点M,N为圆心、大于$\frac{1}{2}$MN长为半径作弧,两弧在第二象限交于点A,若点A的坐标为($\frac{m+1}{2}$,$\frac{m+9}{3}$-1),求点A的坐标.
在平面直角坐标系中,在x轴的负半轴与y轴的正半轴上分别截取OM,ON,使OM=ON;再分别以点M,N为圆心、大于$\frac{1}{2}$MN长为半径作弧,两弧在第二象限交于点A,若点A的坐标为($\frac{m+1}{2}$,$\frac{m+9}{3}$-1),求点A的坐标.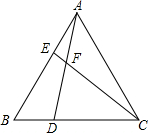 如图,在△ABC中,∠BAC=∠B=60°,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F,当点D、E在边BC、AB上运动时,∠DFC的度数是否发生变化?若不变,求出其度数;若变化,写出其变化规律.
如图,在△ABC中,∠BAC=∠B=60°,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F,当点D、E在边BC、AB上运动时,∠DFC的度数是否发生变化?若不变,求出其度数;若变化,写出其变化规律.