题目内容
2.今年3月20日,“2016重庆国际马拉松赛”在南滨路如期举行,马拉松爱好者张老师作为业余组选手也参与了此次马拉松全程比赛.专业组选手上午8点准时出发,30分钟后张老师出发;在冠军选手到达终点一个半小时后,张老师抵达终点.已知马拉松全程约为42千米,张老师的平均速度是冠军选手的$\frac{2}{3}$.(1)求冠军选手和张老师的平均速度分别为多少?
(2)若明年张老师参加马拉松比赛的起跑时间不变,他计划不超过中午十一点抵达终点,则张老师今年必须加强跑步锻炼,使明年参加比赛时的平均速度至少比今年的平均速度提高百分之多少才能完成计划?
分析 (1)根据题意可以列出相应的方程,然后根据解分式方程的方法即可解答本题;
(2)根据题意可以列出相应的不等式,从而可以解答本题.
解答 解:(1)设冠军选手的速度为x千米/时,
$\frac{42}{x}+(1.5-\frac{30}{60})=\frac{42}{\frac{2}{3}x}$,
解得,x=21,
经检验x=21是原分式方程的解,
∴$\frac{2}{3}x=14$,
即冠军选手的速度是21千米/时,张老师的平均速度是14千米/时;
(2)设张老师明年参加比赛时的平均速度比今年的平均速度提高x%,
$\frac{42}{14(1+x%)}≤11-8.5$,
解得,x≥25,
即张老师明年参加比赛时的平均速度至少比今年的平均速度提高25%,才能完成计划.
点评 本题考查分式方程的应用,一元一次不等式的应用,解答此类问题的关键是明确题意,列出相应的分式方程和不等式,注意分式方程要检验,张老师的出发时间比专业队员晚半小时.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
7. 已知线段AB=4cm,过点B作BC⊥AB,且BC=2cm,连结AC,以C为圆心,CB为半径作弧,交AC于D;以A为圆心,AD为半径作弧,交AB于P,量一量线段AP的长,约为( )
已知线段AB=4cm,过点B作BC⊥AB,且BC=2cm,连结AC,以C为圆心,CB为半径作弧,交AC于D;以A为圆心,AD为半径作弧,交AB于P,量一量线段AP的长,约为( )
 已知线段AB=4cm,过点B作BC⊥AB,且BC=2cm,连结AC,以C为圆心,CB为半径作弧,交AC于D;以A为圆心,AD为半径作弧,交AB于P,量一量线段AP的长,约为( )
已知线段AB=4cm,过点B作BC⊥AB,且BC=2cm,连结AC,以C为圆心,CB为半径作弧,交AC于D;以A为圆心,AD为半径作弧,交AB于P,量一量线段AP的长,约为( )| A. | 2cm | B. | 2.5cm | C. | 3cm | D. | 3.5cm |
14.将四根长度相等的铁丝首尾顺次相接,连成四边形ABCD,转动这个四边形可以使它的形状改变,当∠B=60°时,如图(1),AC=$\sqrt{2}$;当∠B=90°时,如图(2),此时AC的长为( )
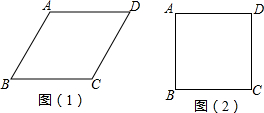
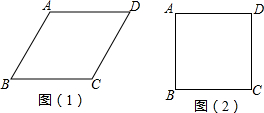
| A. | $2\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
12.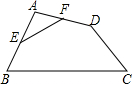 如图,在四边形ABCD中,E、F分别是AB、AD中点,若EF=2,BC=5,CD=3,则tanC等于( )
如图,在四边形ABCD中,E、F分别是AB、AD中点,若EF=2,BC=5,CD=3,则tanC等于( )
 如图,在四边形ABCD中,E、F分别是AB、AD中点,若EF=2,BC=5,CD=3,则tanC等于( )
如图,在四边形ABCD中,E、F分别是AB、AD中点,若EF=2,BC=5,CD=3,则tanC等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
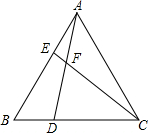 如图,在△ABC中,∠BAC=∠B=60°,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F,当点D、E在边BC、AB上运动时,∠DFC的度数是否发生变化?若不变,求出其度数;若变化,写出其变化规律.
如图,在△ABC中,∠BAC=∠B=60°,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F,当点D、E在边BC、AB上运动时,∠DFC的度数是否发生变化?若不变,求出其度数;若变化,写出其变化规律. 如图,AD=2,AB=4,∠DAB=45°,BD=BC,BD⊥BC,则AC=6.
如图,AD=2,AB=4,∠DAB=45°,BD=BC,BD⊥BC,则AC=6.