题目内容
8.已知,直线AB∥DC,点P为平面上一点,连接AP与CP.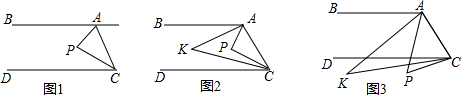
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
分析 (1)先过P作PE∥AB,根据平行线的性质即可得到∠APE=∠BAP,∠CPE=∠DCP,再根据∠APC=∠APE+∠CPE=∠BAP+∠DCP进行计算即可;
(2)过K作KE∥AB,根据KE∥AB∥CD,可得∠AKE=∠BAK,∠CKE=∠DCK,进而得到∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,同理可得,∠APC=∠BAP+∠DCP,再根据角平分线的定义,得出∠BAK+∠DCK=$\frac{1}{2}$∠BAP+$\frac{1}{2}$∠DCP=$\frac{1}{2}$(∠BAP+∠DCP)=$\frac{1}{2}$∠APC,进而得到∠AKC=$\frac{1}{2}$∠APC;
(3)过K作KE∥AB,根据KE∥AB∥CD,可得∠BAK=∠AKE,∠DCK=∠CKE,进而得到∠AKC=∠AKE-∠CKE=∠BAK-∠DCK,同理可得,∠APC=∠BAP-∠DCP,再根据角平分线的定义,得出∠BAK-∠DCK=$\frac{1}{2}$∠BAP-$\frac{1}{2}$∠DCP=$\frac{1}{2}$(∠BAP-∠DCP)=$\frac{1}{2}$∠APC,进而得到∠AKC=$\frac{1}{2}$∠APC.
解答 解:(1)如图1,过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=∠BAP,∠CPE=∠DCP,
∴∠APC=∠APE+∠CPE=∠BAP+∠DCP=60°+20°=80°;
(2)∠AKC=$\frac{1}{2}$∠APC.
理由:如图2,过K作KE∥AB,
∵AB∥CD,
∴KE∥AB∥CD,
∴∠AKE=∠BAK,∠CKE=∠DCK,
∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP+∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴∠BAK+∠DCK=$\frac{1}{2}$∠BAP+$\frac{1}{2}$∠DCP=$\frac{1}{2}$(∠BAP+∠DCP)=$\frac{1}{2}$∠APC,
∴∠AKC=$\frac{1}{2}$∠APC;
(3)∠AKC=$\frac{1}{2}$∠APC.
理由:如图3,过K作KE∥AB,
∵AB∥CD,
∴KE∥AB∥CD,
∴∠BAK=∠AKE,∠DCK=∠CKE,
∴∠AKC=∠AKE-∠CKE=∠BAK-∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP-∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴∠BAK-∠DCK=$\frac{1}{2}$∠BAP-$\frac{1}{2}$∠DCP=$\frac{1}{2}$(∠BAP-∠DCP)=$\frac{1}{2}$∠APC,
∴∠AKC=$\frac{1}{2}$∠APC.
点评 本题主要考查了平行线的性质以及角平分线的定义的运用,解决问题的关键是作平行线构造内错角,依据两直线平行,内错角相等进行计算.

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案| A. | (2,-7) | B. | (-4,7) | C. | (4,-7) | D. | (-2,7) |
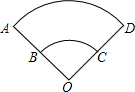 如图,已知扇形OBC、OAD的半径之间的关系是OA=2OB,那么弧AD长是弧BC长的( )
如图,已知扇形OBC、OAD的半径之间的关系是OA=2OB,那么弧AD长是弧BC长的( )| A. | 2倍 | B. | 4倍 | C. | $\frac{1}{2}$倍 | D. | $\frac{1}{4}$倍 |
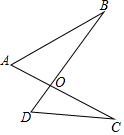 如图,不能判定△AOB和△DOC相似的条件是( )
如图,不能判定△AOB和△DOC相似的条件是( )| A. | AO•CO=BO•DO | B. | $\frac{AO}{DO}=\frac{AB}{CD}$ | C. | ∠A=∠D | D. | ∠B=∠C |

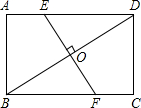 如图矩形ABCD中,AB=3cm,AD=4cm,过对角线BD的中点O作BD的垂直平分线EF,分别交AD、BC于点E、F,则AE的长为$\frac{7}{8}$cm.
如图矩形ABCD中,AB=3cm,AD=4cm,过对角线BD的中点O作BD的垂直平分线EF,分别交AD、BC于点E、F,则AE的长为$\frac{7}{8}$cm.