题目内容
14．在△ABC中，∠A+∠B=∠C，∠B=2∠A，求∠A、∠B、∠C的度数．分析 根据三角形的内角和定理列方程组，直接求∠A、∠B、∠C的度数即可．
解答 解：根据题意得$\left\{\begin{array}{l}{∠A+∠B=∠C}\\{∠B=2∠A}\\{∠A+∠B+∠C=180°}\end{array}\right.$
解得：∠A=30°，∠B=60°，∠C=90°．
点评 本题考查了三角形内角和定理的应用，解决本题的关键是掌握三角形的内角和为180°．
练习册系列答案
名校课堂系列答案
相关题目
2．
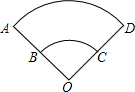如图，已知扇形OBC、OAD的半径之间的关系是OA=2OB，那么弧AD长是弧BC长的（ ）
如图，已知扇形OBC、OAD的半径之间的关系是OA=2OB，那么弧AD长是弧BC长的（ ）| A． | 2倍 | B． | 4倍 | C． | $\frac{1}{2}$倍 | D． | $\frac{1}{4}$倍 |
如图，∠ACB为钝角，用尺规作出△ABC的边AC上的高（不写作法，但要保留作图痕迹）
19．
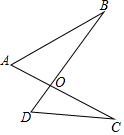如图，不能判定△AOB和△DOC相似的条件是（ ）
如图，不能判定△AOB和△DOC相似的条件是（ ）| A． | AO•CO=BO•DO | B． | $\frac{AO}{DO}=\frac{AB}{CD}$ | C． | ∠A=∠D | D． | ∠B=∠C |
3．
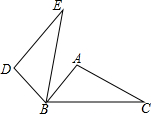如图，△ABC中，∠ABC=40°，∠C=30°，将△ABC绕点B逆时针旋转α（0°＜α≤90°）得到△DBE，若DE∥AB，则α为（ ）
如图，△ABC中，∠ABC=40°，∠C=30°，将△ABC绕点B逆时针旋转α（0°＜α≤90°）得到△DBE，若DE∥AB，则α为（ ）| A． | 50° | B． | 70° | C． | 80° | D． | 90° |