题目内容
1．
已知二次函数y=ax2+bx+c（a≠0）的顶点坐标是（-1，-5.2）及部分图象（如图），由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1，x2，若x1=1.3，则x2的值为（ ）| A． | -1.3 | B． | -2.3 | C． | -0.3 | D． | -3.3 |
分析 利用顶点坐标与两根之和公式可以求出方程的另一根．
解答 解：∵二次函数y=ax2+bx+c的顶点坐标（-1，-5.2）
∴对称轴为x=-1，即-$\frac{b}{2a}$=-1，
∴-$\frac{b}{a}$=-2，
∵x1x2是一元二次方程ax2+bx+c=0的两根，
∴x1+x2=-$\frac{b}{a}$，
又∵x1=1.3
∴x1+x2=1.3+x2=-2
解得：x2=-3.3．
故选：D．
点评 本题考查了抛物线与x轴的交点、抛物线的顶点坐标；熟悉二次函数的顶点坐标公式与一元二次方程两根之和的关系是解决问题的关键．
练习册系列答案
相关题目
由一些大小相同、边长为1cm的小正方形组成的几何体的三视图如图所示，那么这个几何体表面积是22cm2，体积是5cm3．
12．若方程组$\left\{\begin{array}{l}{2a-3b=13}\\{3a+5b=30}\end{array}\right.$的解是$\left\{\begin{array}{l}{a=8.3}\\{b=1.2}\end{array}\right.$，则方程组$\left\{\begin{array}{l}{2（x+2）-3（y-1）=13}\\{3（x+2）+5（y-1）=30}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}{x=8.3}\\{y=1.2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=10.3}\\{y=1.2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=6.3}\\{y=2.2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=10.3}\\{y=0.2}\end{array}\right.$ |
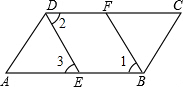如图，∠ABC=∠ADC，BF、DE分别平分∠ABC与∠ADC，DE∥FB．求证：AB∥DC．
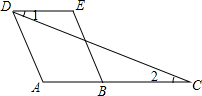请将下列推理过程补充完整．
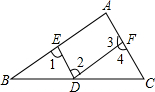如图，下列条件：①∠1=∠2；②∠A=∠4；③∠1=∠4；④∠A+∠3=180°；⑤∠C=∠BDE，其中能判定AB∥DF的有（ ）